法国为什么数学这么强？

建议知乎上各位数学爱好者去看看《线性代数的艺术》，一共只有12页纸，其中一半都是图解，小白也不用担心看不懂！

这份笔记在GitHub登上了热榜，获得了4k+次star。

笔记是基于MIT大牛Gilbert Strang教授的《每个人的线性代数》制作的。

《线性代数的艺术》完整版PDF：https://pan.quark.cn/s/21a7f8ec1597
备用链接：https://pan.xunlei.com/s/VNgU5wuaDrnVcvQAU-bXmN3WA1?pwd=gv69#

日本学者Kenji Hiranabe把这部368页的巨著浓缩成图解，制成了这套笔记并免费开源，后被国内网友kf liu翻译成了中文。

结果不仅在GitHub上反响很好，还得到了原作者的肯定，被收录进了原书介绍页面的interesting link。

甚至Strang还为这份笔记题写了一段前言。

下面就来一起看看这份被原书作者点赞的笔记都讲了些什么吧！

内容介绍

开始介绍之前，先来看看线性代数的世界是什么样子的~

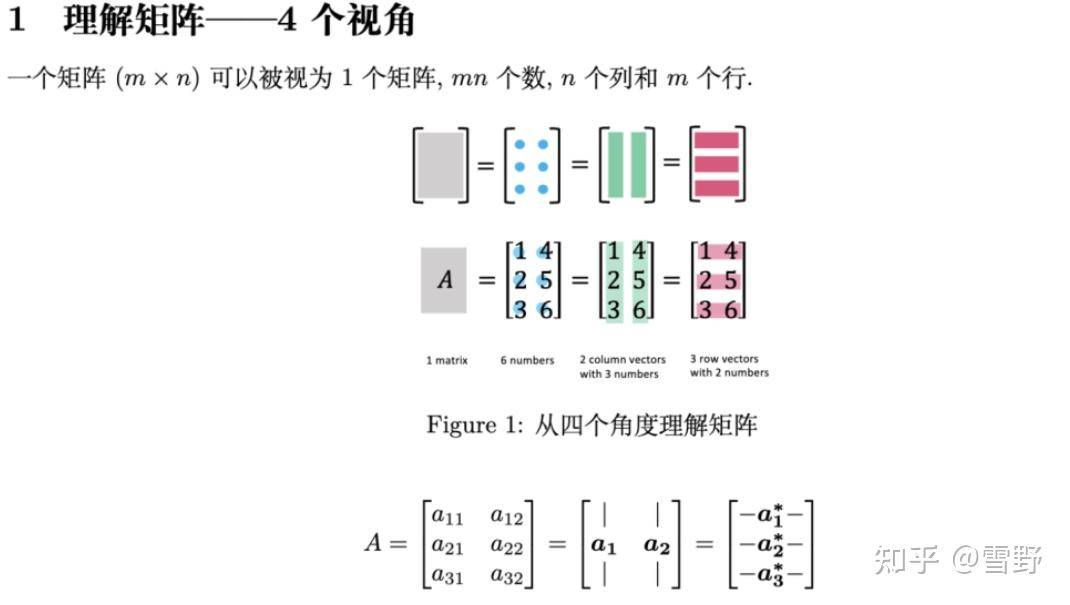
从这张图中我们不难看出，有关线性代数的一切都离不开一个基本概念——矩阵。

因此这份笔记正是从理解矩阵开始的，在这一环节一共展示了4个视角。

有了矩阵的概念之后，作者接着由浅入深地介绍了一些运算方式。

作者依旧是用图的形式讲解，并从不同的视角进行分析，具体包括：

• 向量乘向量
• 矩阵乘向量
• 矩阵乘矩阵

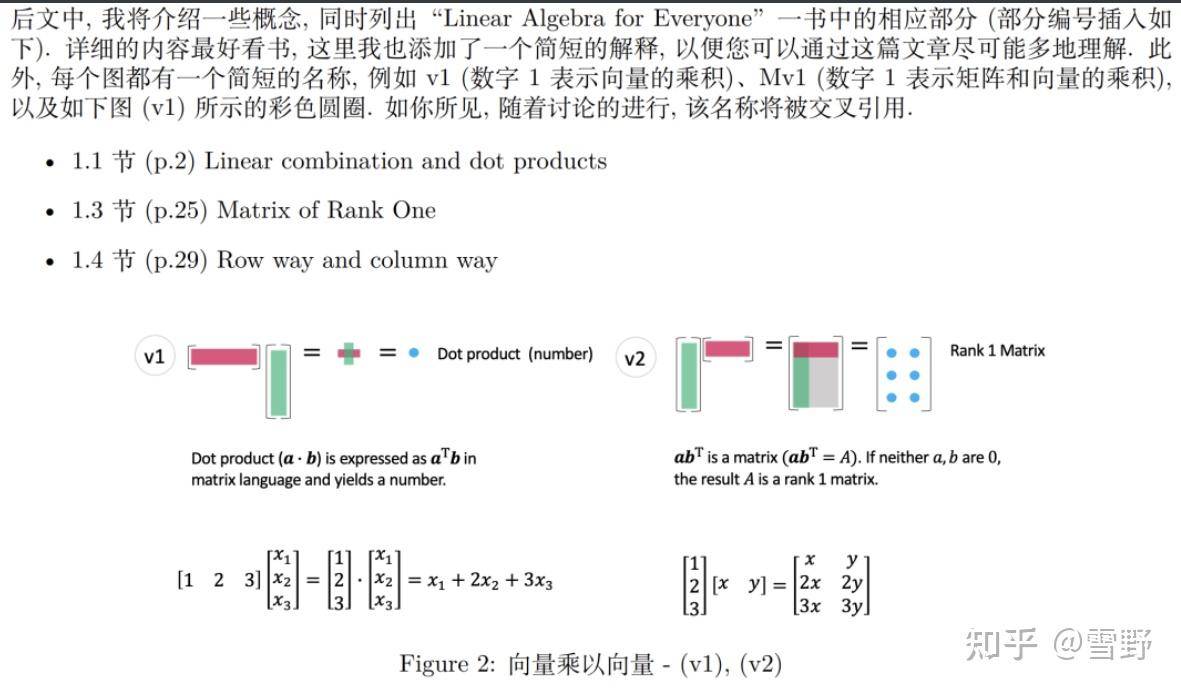
这里我们展示一下最简单的向量乘向量：

基本的运算方式往往是最正确的，但不一定是最高效的。

所以这份笔记接着展示了一些实用技巧。

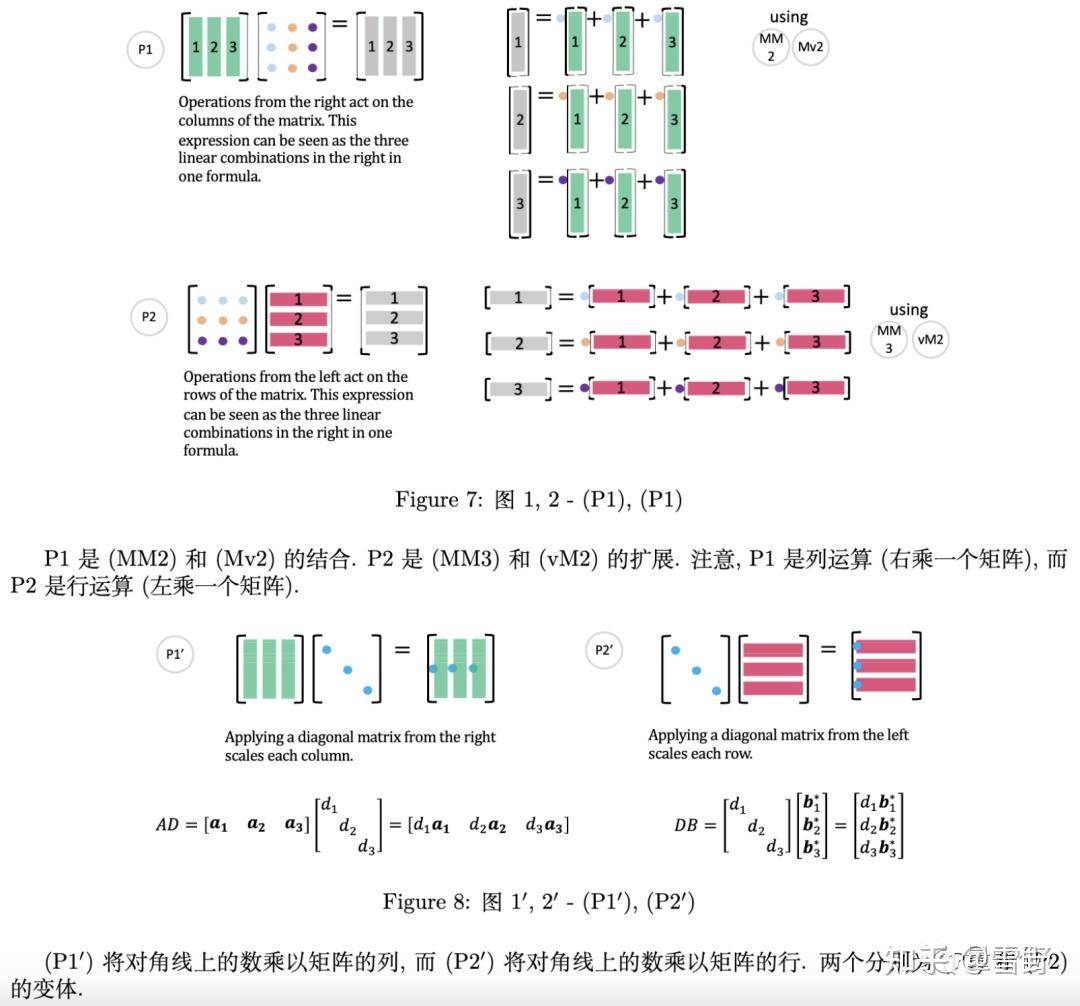
这项技巧还可以用于微分方程的求解。

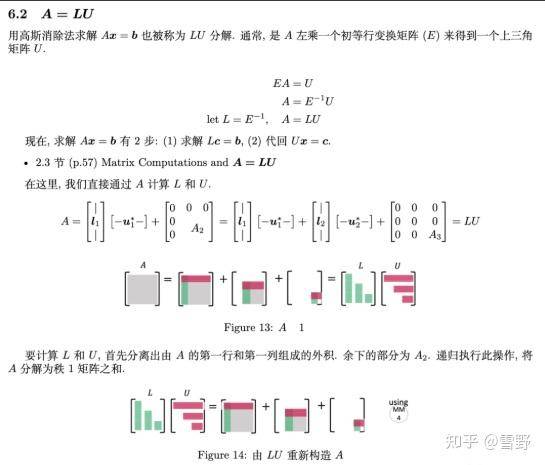
此外，这份笔记还介绍了矩阵的五种分解方式：

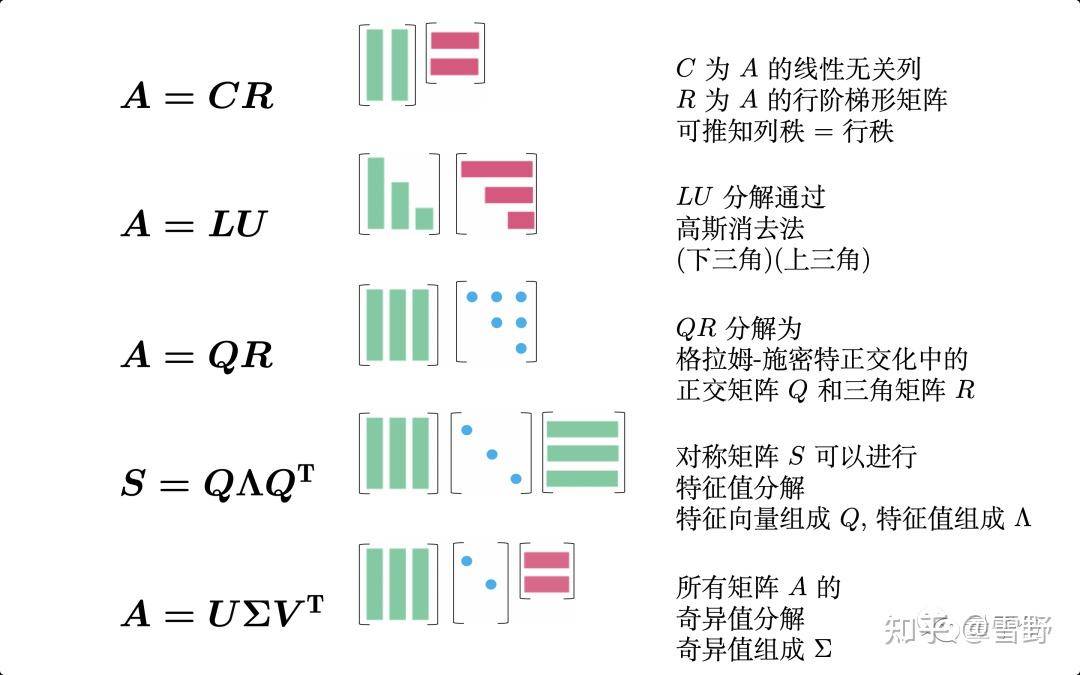
针对以上每种分解方式，还有具体的讲解：

笔记的最后，作者还附上了一张矩阵的特征值映射图。

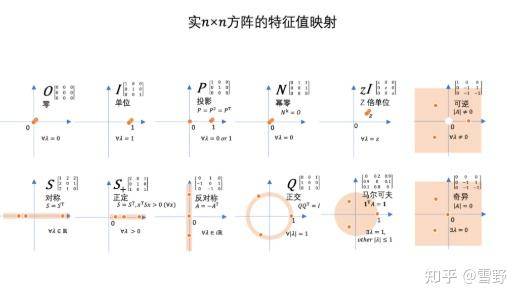
怎么样，看了之后是不是感觉很容易理解？

附上《线性代数的艺术》完整版PDF：https://pan.quark.cn/s/21a7f8ec1597

备用链接：https://pan.xunlei.com/s/VNgU5wuaDrnVcvQAU-bXmN3WA1?pwd=gv69#

另外大家可以看看这本书籍——《微分几何》

这本书只有225页，但它却能带你踏上一段精彩的学习之旅。作者通过一个叫Beng的角色和他的朋友们的故事，把微分几何中那些看似零散的概念串联起来，让整个学习过程变得有趣又连贯。你将会从从欧几里得空间的基础知识出发，逐步深入到曲面和内蕴几何的世界。

书籍PDF免费获取链接

https://pan.quark.cn/s/21a7f8ec1597

最棒的是，这本书不仅仅是带你入门，它还会带你探索Ricci曲率的典型应用，比如探索爱因斯坦方程，推导出史瓦西解，甚至计算出非旋转黑洞的事件视界。这些内容听起来是不是很酷呢？

书中的习题都是精心设计的，每个习题都有详细的解答，确保你在每个学习阶段都能得到充分的指导。这些习题和解答，就像是你的私人教练，确保你在微分几何的健身房里，每一步都走得稳稳的。

这本书是基于一系列面向广泛受众的课程讲义编写的，它已经在课堂上经过了实践检验，证明了自己作为入门和启发性教材的有效性。不管你是学生、研究人员，还是单纯的几何爱好者，这本书都能帮你打下坚实的基础，为未来学习更高级的概念做好充分准备。