2的多少次方的最高位是9？
已经有不少回答给出了答案：2 的 53 次方，首位初次出现 9。
我们现在来探究一下此类问题的通法：给定一个底数 
和一个前缀 ，那么使得 以 开头的最小的自然数 是多少？
问题的抽象
我们放到对数域中来研究：一个数 的开头几位是哪些数字，其实蕴含在 的小数部分里面。用 表示 的小数部分，则「 以 开头」这个条件，可以表示成： 这里面，左右两个端点可以进一步抽象成一个区间 ，而中间的 可以进一步抽象成 ，其中 是一个常数。也就是说，我们的问题转化为：给定一个常数 和一个区间 ，使得 的最小的 是多少？
在原始问题中，各个参数的取值为： 。
画图观察
我们以编号 为横坐标， 为纵坐标，画出 范围内所有的点。其中 的区域用蓝色背景标出，落在此区域内的第一个点的编号就是我们要的答案。
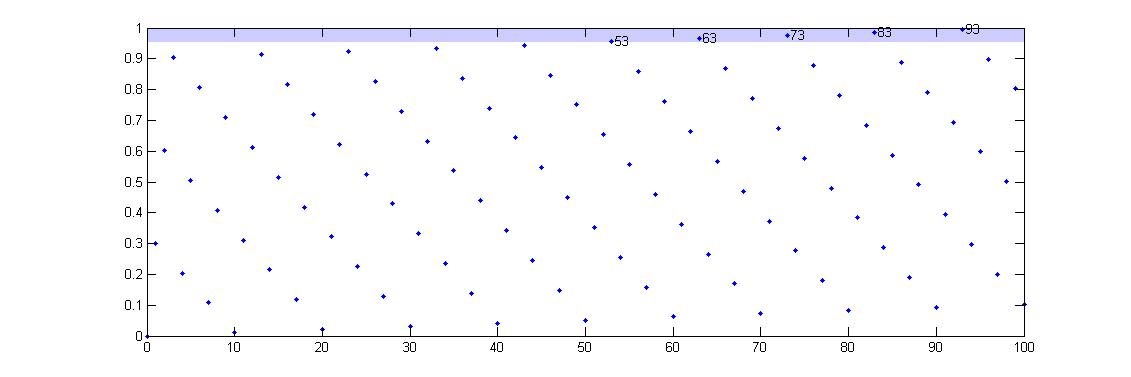
可以看到，这些点似乎形成一条条向右下延伸的斜线，这些斜线在纵轴上的截距分别为 。形成这种现象的原因在于 。能不能利用这些斜线按图索骥，找到哪些点会落在目标区域里呢？似乎不太行——每条斜线上的点的间距太大了，以至于许多斜线直接「跨过」了目标区域，我们没法预知哪条斜线上会有点落在目标区域里。
我们再多画一些点，把 的点全都画出来：
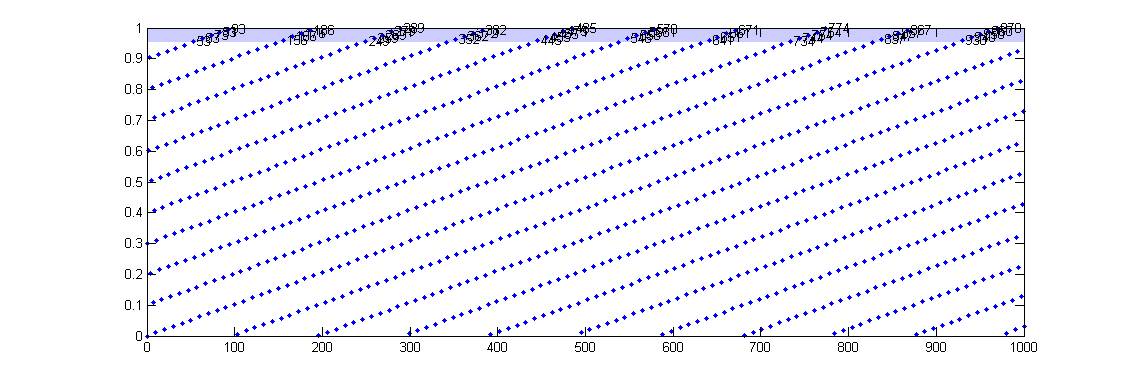
这回，我们看到了另一种斜线模式：它们向右上延伸，在纵轴上的截距分别为 。形成这种模式的原因在于 ，其分母为 10。原来那些向右下延伸的斜线其实依然存在，只不过在图 2 的尺度下，它们的点间距太大，导致它们不如向右上延伸的斜线显著。向右上延伸的这些斜线上的点足够密了，以至于随便选取一条斜线，它们都能够在目标区域里留下足迹。我们只需要找起点离目标区域最近的那条斜线（从 0.9 出发的那条），然后找到它落在目标区域里的第一个点即可。
丢番图逼近
我们发现，常数 的每一个分数形式的近似值 （例如 ），都会在某种尺度下形成比较显著的斜线模式。把纵轴看成循环的，则这样的斜线一共有 条。它们与纵轴的交点（下面称为「起点」）的纵坐标都是 的形式，其中 称为斜线的编号。斜线上相邻两个点的编号相差 ，在纵向的距离是 。这个纵向距离可以作为 对 的逼近误差的一种量度。我们希望找到一个足够好的近似，使得误差不超过目标区间的宽度，即 ，这样就能保证每条斜线上都有点落在目标区域里。同时，这个近似的分母 也不用太大，够用就行。
丢番图逼近的理论告诉我们，可以把 写成连分数的形式： 把这个连分数在任意位置截断，都可以得到 的一个近似值，称为「丢番图逼近」。例如， 的前几个丢番图逼近为： 。这些丢番图逼近，正是 的「第二类最佳逼近」：按 定义的误差，在所有分母不超过 的分数中是最小的。
顺便提一下，逼近误差还可以定义成
我们在所有的「第二类最佳逼近」中，选取第一个满足误差 的近似值。对于 来说，这个近似值是 ，它的误差约为 ，小于目标区间的宽度（约为 ）。
选定了 的一个近似值 后，我们来看看第一个落在目标区域里的点，有希望落在哪些斜线上。起点本来就在目标区域里（即 ）的斜线，自然是有戏的。除此之外，若斜线是上升的，那么起点刚好低于目标区域的那条斜线也有戏；若斜线是下降的，那么起点刚好高于目标区域的那条斜线也有戏。我们可以在这些斜线上寻找答案的候补：
- 对于起点本来就是目标区域里的斜线，我们要找到它上面的第一个点。当然，这个点有可能已经跑到了目标区域之外，所以需要检验。
- 对于起点刚好在目标区域之外的斜线，我们要找到它上面第一个落在目标区域里的点。为此，我们要首先找到斜线上的第一个点，然后按向量 去推出余下的点的坐标，并算出第一个落在目标区域里的点是谁。
总之，现在我们面临的一个问题是：如何求出 号斜线上第一个点的编号？
裴蜀等式 与 数论倒数
不难发现， 号点位于 号斜线上。于是， 号斜线上的第一个点的编号，就是使得 的最小的 。这个方程也可以写成 ，称为「裴蜀等式」，其中 是已知数， 是未知数。它的解可以利用扩展欧几里得算法求出。特别地，我们可以先求出 时的解 ，这样就能很方便地得到 取任意值时的解 。这里， 称为 在模 下的数论倒数。
对于 来说，由于 ，所以 3 在模 10 下的数论倒数为 7。
由于没有任意一条斜线的起点位于目标区域内，而斜线是上升的，所以我们考虑起点刚好低于目标区域的 9 号斜线。它上面的第一个点的编号是 ，纵坐标是 ，到目标区域的距离是 。在这条斜线上，每往后推一个点，编号增加 10，纵坐标增加 。于是，往后推 个点后，就会落在目标区域里，而这个点的编号就是 53。
Show Me the Code
可以把上面的整套流程总结成程序：
import math
import sys
def cont_frac(x, max_levels=10):
"""
求 x 的连分数表示，最多 max_levels 层。
例如：cont_frac(math.log10(2)) = [0, 3, 3, 9, 2, 2, 4, 6, 2, 1]。
"""
result = []
while len(result) < max_levels:
if abs(x - round(x)) < 1e-9:
# 若当前层的值足够接近整数，那就认为是整数
result.append(round(x))
break
result.append(int(x))
x = 1 / (x % 1)
return result
def fold_cont_frac(cont_frac):
"""
把连分数化成分数。
例如：fold_cont_frac([0, 3, 3]) = (3, 10)，代表 0 + 1 / (3 + 1 / 3) = 3/10。
"""
n, d = cont_frac[-1], 1
for a in cont_frac[-2::-1]:
n, d = a * n + d, n
return n, d
def mod_inv(p, q):
"""
用扩展欧几里得算法求 p 在模 q 下的数论倒数。
例如：mod_inv(3, 10) = 7。
"""
old_r, r = p, q
old_s, s = 1, 0
while r != 0:
q = old_r // r
old_r, r = r, old_r - q * r
old_s, s = s, old_s - q * s
return old_s
def min_power(base, target):
"""
求最小的自然数 n，使得 base ** n 以 target 开头。
例如：min_power(2, 3) = 5，因为 2 ** 5 = 32 以 3 开头。
base 可以是任意正实数，target 可以是任意多位正整数。
"""
# 求对数域下的目标区间 [s,t)
# 因为该区间左闭右开，故将两端均减去一个微小的值，
# 以确保与区间端点进行比较时，s 落在区间内，t 落在区间外
c = math.log10(base) % 1
s, t = math.log10(target), math.log10(target + 1)
offset = math.floor(s) + 1e-12
s, t = s - offset, t - offset
# 求 c 的丢番图逼近，使得误差 err 的绝对值不超过 t - s
cf = cont_frac(c)
for levels in range(2, len(cf) + 1):
p, q = fold_cont_frac(cf[:levels])
err = q * c - p
if abs(err) <= t - s:
break
else:
raise ValueError("找不到足够好的丢番图逼近")
# 求 p 在模 q 下的数论倒数 n1
n1 = mod_inv(p, q)
# 编号从 min_k 至 max_k 的斜线，起点在目标区间内。
# 若这些斜线上的第一个点也在目标区间内，则可作为答案的候补。
min_k, max_k = math.ceil(s * q), math.ceil(t * q) - 1
min_n = float("inf")
for k in range(min_k, max_k + 1):
n = (n1 * k) % q # 斜线上第一个点的编号
y = (n * c) % 1 # 斜线上第一个点的纵坐标
if s <= y < t and n < min_n:
min_n = n
# 若斜线向上，则答案也可能在 min_k 下面一条斜线上
if err > 0 and s > 0:
k = min_k - 1
n = (n1 * k) % q # 斜线上第一个点的编号
y = (n * c) % 1 # 斜线上第一个点的纵坐标
n += q * math.ceil((s - y) / err) # 目标区域内第一个点的编号
if n < min_n:
min_n = n
# 若斜线向下，则答案也可能在 max_k 上面一条斜线上
elif err < 0:
k = max_k + 1
n = (n1 * k) % q
# 由于斜线向下，故对于 0 号点，认为其纵坐标为 1 而非 0
y = (n * c) % 1 or 1
n += q * (math.floor((y - t) / (-err)) + 1)
if n < min_n:
min_n = n
# 返回落在目标区间内的点的最小编号
return min_n
来试验一下，2 的几次方的初次以 1 ~ 9 开头：
>>> for i in range(1, 10):
... n = min_power(2, i)
... print(f"2 ** {n} == {2 ** n}")
2 ** 0 == 1
2 ** 1 == 2
2 ** 5 == 32
2 ** 2 == 4
2 ** 9 == 512
2 ** 6 == 64
2 ** 46 == 70368744177664
2 ** 3 == 8
2 ** 53 == 9007199254740992
果然印证了原题的答案： 初次以 9 开头。
还可以试验一下 2 的几次方初次以 10 ~ 99 开头。注意对于 10，程序给出的结果是 ，因为 1（即 1.0）也可以认为是以 10 开头。20、40、80 同理。
>>> for i in range(10, 100):
... n = min_power(2, i)
... print(f"2 ** {n} == {2 ** n}")
2 ** 0 == 1
2 ** 50 == 1125899906842624
2 ** 7 == 128
2 ** 17 == 131072
2 ** 47 == 140737488355328
2 ** 77 == 151115727451828646838272
2 ** 4 == 16
2 ** 34 == 17179869184
2 ** 54 == 18014398509481984
2 ** 84 == 19342813113834066795298816
2 ** 1 == 2
2 ** 31 == 2147483648
2 ** 51 == 2251799813685248
2 ** 61 == 2305843009213693952
2 ** 81 == 2417851639229258349412352
2 ** 8 == 256
2 ** 18 == 262144
2 ** 38 == 274877906944
2 ** 48 == 281474976710656
2 ** 68 == 295147905179352825856
2 ** 78 == 302231454903657293676544
2 ** 98 == 316912650057057350374175801344
2 ** 5 == 32
2 ** 25 == 33554432
2 ** 35 == 34359738368
2 ** 45 == 35184372088832
2 ** 55 == 36028797018963968
2 ** 75 == 37778931862957161709568
2 ** 85 == 38685626227668133590597632
2 ** 95 == 39614081257132168796771975168
2 ** 2 == 4
2 ** 22 == 4194304
2 ** 32 == 4294967296
2 ** 42 == 4398046511104
2 ** 145 == 44601490397061246283071436545296723011960832
2 ** 52 == 4503599627370496
2 ** 62 == 4611686018427387904
2 ** 72 == 4722366482869645213696
2 ** 82 == 4835703278458516698824704
2 ** 92 == 4951760157141521099596496896
2 ** 102 == 5070602400912917605986812821504
2 ** 9 == 512
2 ** 19 == 524288
2 ** 29 == 536870912
2 ** 39 == 549755813888
2 ** 142 == 5575186299632655785383929568162090376495104
2 ** 49 == 562949953421312
2 ** 59 == 576460752303423488
2 ** 162 == 5846006549323611672814739330865132078623730171904
2 ** 69 == 590295810358705651712
2 ** 79 == 604462909807314587353088
2 ** 89 == 618970019642690137449562112
2 ** 192 == 6277101735386680763835789423207666416102355444464034512896
2 ** 99 == 633825300114114700748351602688
2 ** 6 == 64
2 ** 16 == 65536
2 ** 119 == 664613997892457936451903530140172288
2 ** 26 == 67108864
2 ** 36 == 68719476736
2 ** 139 == 696898287454081973172991196020261297061888
2 ** 46 == 70368744177664
2 ** 149 == 713623846352979940529142984724747568191373312
2 ** 56 == 72057594037927936
2 ** 66 == 73786976294838206464
2 ** 169 == 748288838313422294120286634350736906063837462003712
2 ** 76 == 75557863725914323419136
2 ** 179 == 766247770432944429179173513575154591809369561091801088
2 ** 86 == 77371252455336267181195264
2 ** 189 == 784637716923335095479473677900958302012794430558004314112
2 ** 96 == 79228162514264337593543950336
2 ** 3 == 8
2 ** 13 == 8192
2 ** 209 == 822752278660603021077484591278675252491367932816789931674304512
2 ** 23 == 8388608
2 ** 219 == 842498333348457493583344221469363458551160763204392890034487820288
2 ** 33 == 8589934592
2 ** 229 == 862718293348820473429344482784628181556388621521298319395315527974912
2 ** 43 == 8796093022208
2 ** 239 == 883423532389192164791648750371459257913741948437809479060803100646309888
2 ** 146 == 89202980794122492566142873090593446023921664
2 ** 53 == 9007199254740992
2 ** 156 == 91343852333181432387730302044767688728495783936
2 ** 63 == 9223372036854775808
2 ** 166 == 93536104789177786765035829293842113257979682750464
2 ** 73 == 9444732965739290427392
2 ** 176 == 95780971304118053647396689196894323976171195136475136
2 ** 83 == 9671406556917033397649408
2 ** 279 == 971334446112864535459730953411759453321203419526069760625906204869452142602604249088
2 ** 186 == 98079714615416886934934209737619787751599303819750539264
2 ** 93 == 9903520314283042199192993792
可以看到，输出的前半段像一棵圣诞树一样错落有致，每一个三角形中，指数的个位数都相同，十位数基本上是依次递增，偶尔会跳过一个数。这背后的原因，就在于 非常接近 10 的整数次幂。在输出的后半段，「指数依次加 10」的模式开始显出一些漏洞，被 等指数更大的幂填充；到了最后，漏洞多到填充它们的幂的指数也显示出了「依次加 10」的规律（例如 到 ）。
还可以换一些数字来玩：
>>> min_power(math.pi, 520)
275
>>> min_power(666, 888)
2000
>>> min_power(114514, 1919810)
1947860
可以验证，确实有：
