为什么银行存款、河流长度等集合的首位数字更容易出现 1 而不是 9?
楼上已有回答说了本福特定律,这里我来大概解释一下它的原理。
事实上,这个问题分为两部分:数学部分和非数学部分,数学部分又分为两部分:动力系统部分和统计学部分。
动力系统部分
数学上这是一个有关随机整数列首位分布的问题。在Stein的 Fourier Analysis 中有讲过Weyl等分布定理(Weyl's euqidistribution theorem)。在遍历论/动力系统中也有一个相关的定理,叫Birkhoff遍历定理(Birkhoff’s Ergodic Theorem)。下面我们来大概梳理一下它们之间的关系。
Weyl等分布定理
下面这位学长曾经写过详细的文章来介绍这件事情:
元亨利贞:{sin(n^p)}稠密性,Weyl准则,等分布序列Equidistributed SequenceBirkhoff遍历定理
内容表述:对于保测动力系统 ,若系统是遍历的(即不存在非平凡的
-不变集),则对任意可积函数
,时间平均几乎处处收敛于空间平均:
这是Weyl等分布定理的推广。至于为什么是推广,如果有空了再写()
本福特定律
我们用一个例子来说明什么是本福特定律。
考察数列
记录它们的首位数字,直观上我们会觉得这是一个随机的排列,从而首位数字为
的概率都相等,即均为 然而事实并非如此。
事实上,映射
是遍历的(ergodic),即满足
这个网页中有所说明。
从而,Weyl等分布定理或者Birkhoff遍历定理告诉我们如下性质:
命题 . 在上述数列中,以 为首位数字的概率是

这直接地告诉我们:用等比数列生成的随机数并不是真随机数,而是一种伪随机数。
我们着重考察具有这种性质的数据,引入如下定义:
定义 . 一组数据如果满足首位数字的概率
则称其满足本福特定律。
注记 . 本福特定律事实上是一个定义而非定理!!!后面会再次重复。
注记 . 还可以对位数进行扩展,譬如 作为第
位数字的概率是
数学部分就到此结束了。事实上数学也只能证明这么多。
统计学部分
本福特定律需要检验
那么(终于)问题来了,题主说的银行存款、河流长度为什么满足本福特定律呢?事实上,本福特定律是一个后验的定义,即我们并不能知道哪些数据事实上满足本福特定律,当然,如果给定了数学表达式。我们可以推导,然而问题是现实生活中的数据往往没有准确的公式来表达。下面是两个例子:
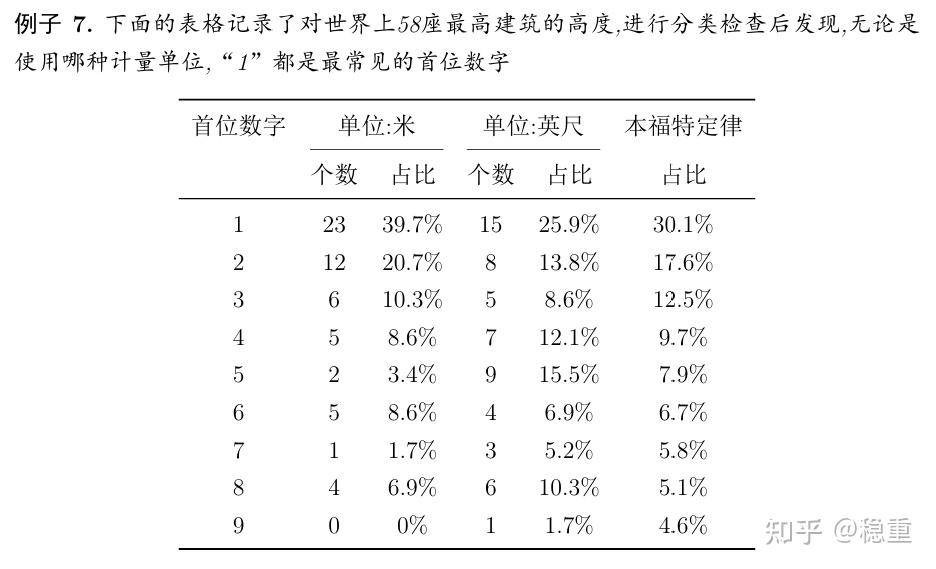
感谢评论区指正,注意上述数据来源于List of tallest buildings and structures - Wikipedia,这里的表格指的是按照不同材料/建筑方式建筑的最高高度!(更新于2025/3/17)
也并非所有的数列都满足本福特定律,例如:
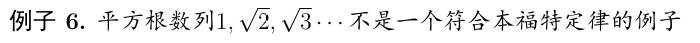
那么最重要的问题就是:什么样的序列满足本福特定律?
因为本福特定律事实上是一个定义而非定理,我们可以考虑用特定的方式检验数据,从而判断其为真随机还是伪随机,如果是真随机,那么就不满足本福特定律,如果是伪随机,且满足本福特分布,才有的谈!
在统计学中,常见的检验方式有二:Kolmogorov-Smirnov test 和 Kuiper's test,详见如下两个链接(均来自Wikipedia):
Kolmogorov–Smirnov test - WikipediaKuiper's test - Wikipedia题主的问题
所以说,在给定一些银行存款,河流长度的数据后,可以使用特定方法检验它是否符合本福特定律的分布。
非数学部分
至于为什么那么多数据都满足本福特定律的分布,乃至于可以检验选举投票、税务、经济发展数据是否造假呢?(见Benford's Law | Brilliant Math & Science Wiki的最后一段)
——暂不清楚,这可能是个哲学问题吧。





