如何看待 Yu Deng 及其合作者在 arXiv 发布对希尔伯特第六问题的解决？

我们莫不是又要见证历史了？作为数学稀烂的物理人，我只能从物理的角度介绍一下希尔伯特第六问题的来龙去脉，数学部分则暂时观望一波。

1900年，在普朗克开启量子时代的同时，希尔伯特在巴黎举行的国际数学家大会上发表了10个（1、2、6、7、8、13、16、19、21 和 22）尚未解决的问题，完整的23个问题后续被出版。Yu Deng老师处理的第六问题正是第一批次的问题之一，其标准叙述为：

物理学公理的数学处理。几何学基础的研究提示了这样的问题：以公理化的方式，对那些数学已发挥重要作用的物理科学（首要的是概率论和力学）进行同样处理。

简单来说就是物理学的公理化问题，希尔伯特本人对这个问题非常看重，也花了很多时间进行研究，他还进一步分析道：

就概率论公理而言，我认为对均值方法在数理物理学（尤其是气体动力学理论）中的发展进行严格且完备的考察，应与其逻辑基础研究同步推进。……关于力学基础，玻尔兹曼的研究提出了这样的数学课题：对其仅作概要说明的极限过程进行严格推演，这些过程将原子论观点与连续介质的运动定律相衔接。

但虽说是物理学公理化，这其实也不是把所有物理学都公理化掉，毕竟量子力学已经被冯诺依曼给公理化了，而更进一步的公理化量子场论也还是现在进行时。希尔伯特在后续讨论中，将问题拆分为两个关键目标：1.概率论的公理化基础（已在20世纪上半叶解决）；2.从原子论到连续介质运动定律的数学极限过程。因此在希尔伯特第六问题中，其核心在于，如何从离散的原子论观点出发进入到连续介质理论，换言之，怎么从牛顿定律出发导出流体力学的基本方程（如纳维-斯托克斯方程）。

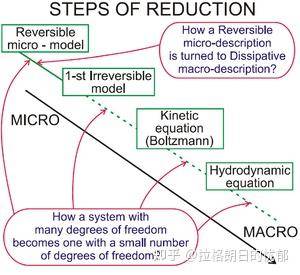
这个问题其实不仅仅是一个数学问题，也涉及到我们对这个世界的基本理解，即世界作为一个整体，不同层次的规律是如何协调在一起的，如果能建立微观粒子系统与宏观连续介质之间的数学桥梁，那么这种协调就可以建立在一个比较坚实的基础之上。这里其实还涉及到一个老生常谈的问题，可逆的牛顿定律是如何变成不可逆的玻尔兹曼方程，时间可逆与不可逆如何转换。当然从物理量子场论的角度，我们对这种协调的理解主要是重整化群和有效场论。从流体力学的角度这个问题也很重要，这可以为湍流等复杂现象提供更底层的理论解释基础。

按照本文作者的叙述^[1]，他们成功通过硬球碰撞粒子系统的弹性碰撞，经由玻尔兹曼动理学方程成功推导出流体力学基本方程，最终实现希尔伯特提出的“从牛顿定律到流体方程”的数学路径。

在希尔伯特1900年的演讲中，他提到

"我们之中有谁不愿揭开未来隐藏的面纱，一睹科学未来的进展与未来世纪发展的奥秘？未来的数学精英们将追求哪些特定目标？在广阔而丰富的数学思想领域中，新世纪又将揭示哪些新方法和新事实？"

如果这次工作被确认无误，那“未来隐藏的面纱”就又被揭下来了一部分，物理学宏观微观的数学联系也会更坚实。