如何从零基础开始自学数学？

匈牙利裔美国数学家乔治·波利亚（1887年12月13日—1985年9月7日）（对，就是那个发明了「波利亚计数定理」的波利亚）写过三本神书，分别是：

• 《怎样解题》(1944)
• 《数学的合情推理（上下两卷：数学中的归纳和类比+合情推理模式）》(1954)
• 《数学的发现》(1962,1965)

这里就简单说说第一本《怎样解题》。

书籍电子版PDF: https://pan.quark.cn/s/21a7f8ec1597

这本书对数学学习者和教育者的意义非常重大，而且小学生都能看懂，强烈建议所有需要学数学的（包括义务教育数学）的人都去下一本读读，读得越早越好。可以极大提高任何阶段数学的学习乐趣、解题能力和考试成绩。我这个80后是本科才知道这本书，悔之晚矣。

于是我有机会就会向其他人推荐这本书，光知乎上就写过至少两个回答。

这本书的初版序（1944年写于斯坦福大学）里有这么一段话：

作者还记得自己的学生时代，那是他还是一个有点雄心的学生，渴望能懂一点数学和物理学。他听课、看书，试图领会所给出的解答及事实。但是有一个问题却一再困扰着他：「是的，这个解答看来是行的，它似乎是正确的，但怎样才能想到这样一个解答呢？是的，这个实验看起来可行，这似乎是事实，但是人们怎么会发现这些事实的？而我自己如何才能想到或发现它们呢？」 如今，作者正在一所大学中教授数学。他认为，或者说他希望，他的一些更努力的学生能提出类似的一些问题，他会尽力去满足他们的好奇心。不仅要尽力去理解这道或那道题目的解答，而且要去理解这个解答的动机和步骤，并尽力向别人解释这些动机和步骤，这就最终导致他写了现在这本书。作者希望本书对于那些期望提高学生解题能力的教师，以及对于渴望提高个人能力的学生都会有用。

另外，西安电子科技大学的博士生导师刘三阳在一次报告中介绍：

欧拉说：「一个科学家如果只是做出了给科学宝库增加财富的发现，而不能坦率阐述那引导他做出发现的思想，那么他就没有给科学做出足够的工作。」 波利亚说：「在前辈数学家中，欧拉对我的影响最大。主要原因在于，欧拉做了一些跟他才能相当的伟大数学家从没有做过的事。即他解释了他是如何发现他的结果的。对此，我如获至宝。」

《怎样解题》这本书里讲述了一种可操作性很强的解题思考步骤。不但学生可以用这些步骤解题，老师也应该积极引导学生遵循这些步骤思考（有些学霸可能自行摸索出、或者在很小的时候被老师或父母培养过这套方法，并在义务教育阶段充分打磨过，从而获得了超强的解题能力）。

在此略微摘录一下这套方法的概述。包含四个步骤。

1. 理解题目。明确未知量、已知数据和条件。
2. 拟定方案（本书核心！）。了解各个项目是如何相关的，未知量和数据之间有什么关系，以得到解题的思路。数学老师以这样一个问题作为开始是很适当的：「你知道一道与它相关的题目吗？」「观察未知量，并尽力想出一道你熟悉的具有相同或相似未知量的题目。」「这里有一道题和你的题目相关而且以前解过。你能利用它吗？」「你能重新叙述这道题目吗？」「如果你不能解出这道题目，先试着解答这道相关的题目。」「你用到所有数据了吗？你用到所有条件了吗？」
3. 执行。执行上一步的计划。
4. 回顾。检查和讨论上一步完成的解答。

由于这本书只有扫描版，所以上面都是我手打的，很不详细，但已经尽量介绍了这本书的特征：不是教具体解法，而是教「想到解法的过程」，而后者可以通用于所有数学问题，甚至所有领域的问题。

最后说一下，波利亚这三本解题神书：《怎样解题》(1944)、《数学的合情推理（上下两卷：数学中的归纳和类比+合情推理模式）》(1954)和《数学的发现》(1962,1965)，都早就翻译成了中文。虽然可以下载电子版，但其实非常建议买实体书，因为捧在手里翻阅的时候，能感受到神级数学家在谆谆善诱地打通你数学思考的任督二脉。

书籍电子版PDF: https://pan.quark.cn/s/21a7f8ec1597

另外推荐一本书——《数学的雨伞下：理解世界的乐趣》。这本书是法国数学学会“达朗贝尔奖”得主的科普名作,其最大的特点是“没有一个公式，却讲透了数学的本质”，读完可以刷新自己对于很多事情的认知。

数学的雨伞下 完整版PDF：https://pan.quark.cn/s/21a7f8ec1597
备用链接：https://pan.xunlei.com/s/VNgU5wuaDrnVcvQAU-bXmN3WA1?pwd=gv69#

这本书只有短短的五章，涉及十几个问题。无论从话题的有趣性，还是没什么数学基础读者的可读性都非常不错，我觉得将读书的过程称之为一场美妙的数学之旅非常合适。它非常好，好到什么程度，就是我看前面想到了一些可能补充的点，但是读到后面发现全都被囊括进去了。唯独的小遗憾可能是整本书的插图都非常“复古”，没那么精美又好像有点糊。不像一些书以没有公式作为卖点，附录中展示了每章真正的数学公式可供参考。

第一篇本福特定律，是个非典型的数字统计规律，我很惊讶它居然能被证明，且可用于检测一些数据造假。从生活中的超市开始的一个小发现，应用范围大的离谱。作者以绝对数值的大小比较，和人类相对感知之间的矛盾说起，将数字按照等间距的乘法进行排布，实际上得到了对数的分布——因为它能将乘法变成加法，还有我们熟知的纳皮尔的白皮书加速了世界的进程的故事。在没有数感的原始人或是动物身上做实验，也得到了类似的结果，从而得到世界可能是乘法的，常用如分贝、pH值等。这个定律也不会因为量度的变化而改变，因为本质上的相对关系是不变的。

第二篇可能有点跑题，海拔是如何定义的？数学里的反例思考有点像抬杠一样，尝试攻击每一个不严谨的地方，这样下去，“所有试图将现实梳理出头绪都可能复杂的令人绝望”。数学在做的事就是将包括数字在内的东西抽象成概念，以至于我们可以用不存在的东西去思考，书名雨伞是贯穿所有问题的思考方式。

海岸线有多长？或是书中所说的边境长度，从各地的数据中发现巨大的差异，此时曼德勃罗（书中译为曼德博）写下了那篇经典文章。在讲无穷大时作者没用经典的希尔伯特旅馆例子，用买巧克力来举例。讲到分形几何就不得不先提到维度，再次呼应了对数的尺度部分。

书中有一句话我很喜欢，“数学不在乎什么是显而易见的，它只想知道什么是真的。”从主观上我不太能接受数学是模糊的，当然这与模糊数学的分支无关，它定义应当是清晰准确的，作者又确实说服了我。他用非常容易的例子逐步引入球面几何。最后一章从光速不变理论到无穷，你可能感觉没学到什么知识，这个例子也许会在你未来学习的时候潜移默化的浮现，这样就足够了的。

研究数学，就是创造想象的世界，在这些世界中，我们的思维可以自由漫步，不必担心现实的妨碍。这种思维方式虽然涵盖的范围要广得多，但和尼普尔人在加法世界中用来简化乘法的思维方式非常相似。当你碰到一个科学问题时，下面这种解决方法往往会很有效：

1. 创造一个数学世界，你可以在这个世界里把问题模型化；

2. 在这个数学世界里解决问题；

3. 把结果转回到现实世界中。

比如说，这种通用的方法就被天文学家用来了解行星的轨迹或预测日食（图 2.8）。

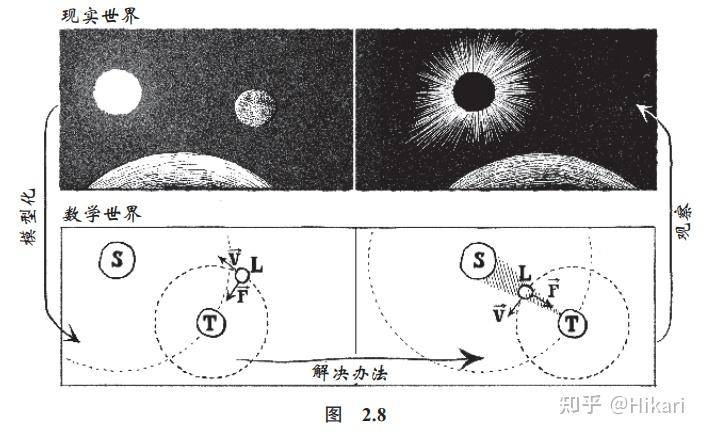
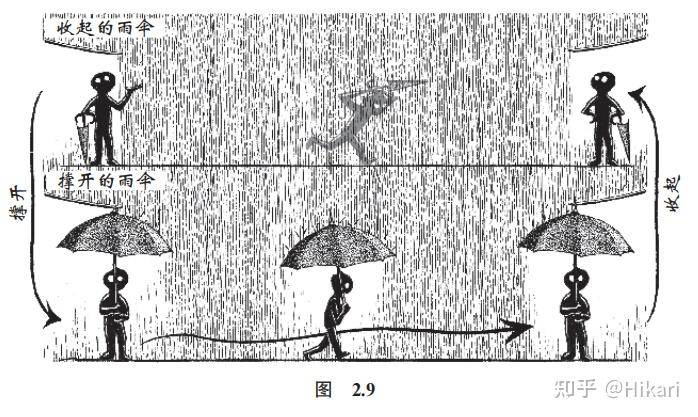
这种解决问题的模式叫作“雨伞定理”。如果你在雨天想要在不被淋湿的情况下从一个地方前往另一个地方，请按照以下步骤操作：

1. 撑开你的雨伞；

2. 开始你的行程；

3. 收起你的雨伞。

步骤 1 和步骤 3 的操作是相反的，如果你能够在雨伞为你打开的特定世界中达成预期的目标，那么你在操作结束时就会恢复到开始时的状态。负数的雨伞为地理学家测量海拔提供了研究上的便利。对数的雨伞让淹没在乘法中的天文学家得以进入加法的世界。而更广泛地说，抽象的雨伞为所有科学家进入数学世界提供了可能。

在接下来的路途中，我们还会用到很多雨伞。雨伞，是观点的改变，是差异，是从另一个角度看待事物的艺术，一种更适合、更有效的角度。

走得更远，并不总是意味着长久而乏味的努力，而是首先要找到解决所面临的问题的正确方法。如果我们以正确的方式看待问题，那么最错综复杂的问题也会在一瞬间变得简单明了。伟大的智者能尽显其才，首先是因为他们拥有在正确的时间发明正确的雨伞的能力。

在 18 世纪，古怪的作家和旅行家乔纳斯·汉韦（Jonas Hanway）是第一个使用雨伞的伦敦人。这是一把真的雨伞——挡雨的伞。他为此遭受了很多白眼和伦敦马车夫赤裸裸的恶意，因为在当时，搭乘马车一直是在糟糕天气出行而不会被淋湿的唯一方法。毫不畏惧旁人眼光的汉韦继续自豪地使用了三十多年的雨伞，并慢慢看到他的同胞们也开始使用雨伞。在他去世后几个月，第一批商业化雨伞出现在英国，并获得了我们今日所知的成功。

不要惧怕与众不同，这就是雨伞的智慧。让我们无所畏惧，既不感到羞耻，也不抱有偏见。一旦接受在头顶撑起抽象的雨伞并进入数学的世界，我们就不会再全然依赖现实。不必让自己陷在无用的限制或令人尴尬的既有观念之中。你想要一个 4 月 34 号吗？拿去吧！你想要负数吗？拿去吧！你想要无穷吗？拿去吧！如果所有这些想法不会干扰你组织思维，甚至还有所帮助，那为什么要剥夺它们呢？你是自由的！

如此自由，甚至容易让人头晕目眩。在这一点上，数学和一大盘点心有着异曲同工之妙——选择太多，就难以做出选择了。懂得如何在数学世界里自我驾驭，是一种需要实践和直觉的能力。

为此，数学家制造出很多导航工具，其中有两个指南针：一个名叫“实用”，一个名叫“优雅”。“实用”引导我们创造出最贴近现实的抽象世界，在这些抽象世界中进行的研究能够轻松地转化为关于我们宇宙的知识。“优雅”告诉我们要完全抛开现实，并沉醉在抽象世界的奇观中。那里有许许多多美丽的事情要做——如果一件事是无用的，那它就更美了。

每个人都能以自己的方式使用这两个指南针。有些人偏爱其中的某一个，有些人则两个一起用，并不断在两个指南针指示的方向之间寻找完美的平衡。但世界充满奥秘，因此，探索实用之人和探索优雅之人常常会在走过不同的道路之后，在同一个地方不期而遇。看到大自然如此喜爱按照优雅的数学原理运转，真是既让人目瞪口呆，又让人不知所措达到

最后附上数学的雨伞下完整版PDF：https://pan.quark.cn/s/21a7f8ec1597