如何评价LLNL推出的开源有限元项目MFEM？

为大家全面介绍模块化有限元代码MFEM的功能和使用技巧。这是我自己整理的，可能是目前全网最全面的MFEM介绍博客，全文约1万字，欢迎点赞、关注、收藏，以便随时查看。
也欢迎你加入MFEM中文社区一起交流、做贡献：
Q群：760401312
Wechat ID: ym_cae（备注MFEM社群

---

MFEM（Modular Finite Element Method）是由美国Lawrence Livermore National Laboratory（全球最强的高性能数值计算中心之一）历时14年（2010-2024，实际上从2002年左右开始预研）开发的支持GPU并行的可扩展有限元计算程序。该程序的开发前后累计投入148人。目前代码量约为50万行。MFEM已于2021年全部开源（发表文章 MFEM: A modular finite element methods library，doi: https://doi.org/10.1016/j.camwa.2020.06.009）。
MFEM基于BSD许可证发行，在申明许可版权的前提下，可用于商业用途。

MFEM - Finite Element Discretization Library

开发负责人

Tzanio Kolev

Tzanio Kolevs是MFEM项目负责人。
Tzanio Kolev 是劳伦斯利弗莫尔国家实验室（Lawrence Livermore National Laboratory, LLNL）应用科学计算中心（ Center for Applied Scientific Computing， CASC）一名计算数学家，他致力于研究高效的有限元离散化和求解器，以解决各种应用领域中出现的问题，例如可压缩冲击流体动力学、多材料任意拉格朗日-欧拉方法（Arbitrary Lagrange-Euler，ALE）仿真、辐射流体动力学和计算电磁学。

Robert Anderson

罗伯特·安德森（Robert Anderson）是CASC的计算科学家，也是ALE-AMR项目的项目负责人。该项目结合了任意拉格朗日-欧拉（ALE）流体动力学求解技术的优势和自适应网格细化（AMR）的效率，利用了CASC开发的SAMRAI面向对象的AMR框架。除了为算法研究和开发提供平台外，ALE-AMR代码正在开发中，以应用于表征国家点火设施（NIF）实验中产生的碎片和弹片的问题。

MFEM功能介绍

MFEM 是一个用于有限元的模块化并行 C++ 库 方法。其目标是实现高性能、可扩展的有限元 离散化研究和应用开发的广泛性 平台，从笔记本电脑到超级计算机。

从概念上讲，MFEM 可以看作是一个有限元工具箱，类似于 MATLAB在线性代数方法中的作用。

高阶有限元空间

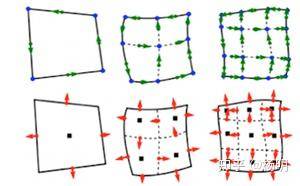
MFEM 支持二维和三维中各种有限元空间，包括任意高阶：

• H1-协调、H(div)-协调、H(curl)-符合空间，
• 间断 L2 空间，
• 数值迹（界面）空间，
• 用于等几何分析的 NURBS 空间。

代码中提供了许多在这些空间上定义的双线性和线性形式，以及梯度、旋度和嵌入这些空间之间的线性算子。

灵活的离散化

除了传统的 Galerkin 方法，MFEM 还支持快速原型设计：

• 混合有限元，
• 不连续 Galerkin (DG) 方法，
• 等几何分析方法，
• 不连续 Petrov-Galerkin (DPG) 方法，
• 高阶问题的混合化和静态凝聚。

广泛的网格类型

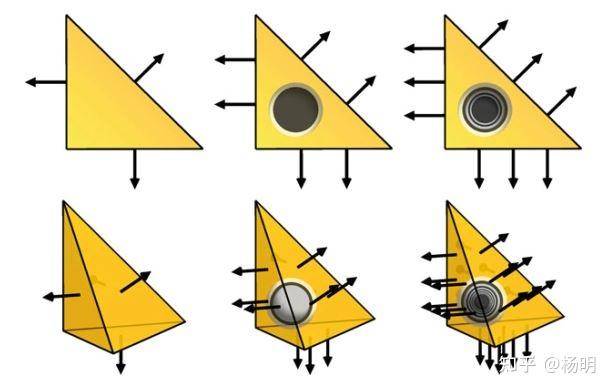
MFEM 支持任意单元变换，并包括处理以下内容的类：

• 三角形、四边形、四面体、楔形和六面体单元，
• 均匀细化（所有元素类型），
• 符合局部网格细化（三角形/四面体网格），
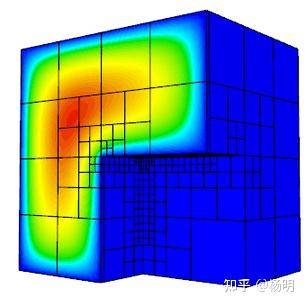
• 不符合网格细化（四边形/六面体网格），包括各向异性细化，
• 基于目标矩阵优化范式 (TMOP) 的网格优化，
• 具有曲面边界的高阶元素，
• 嵌入在 3D 中的表面网格，拓扑周期性网格，1D 网格。

通过与 PUMI 分布式网格管理系统的集成，为简单网格上的自动化自适应分析和平面孔洞并行修改提供额外支持。

并行化、可扩展且支持 GPU

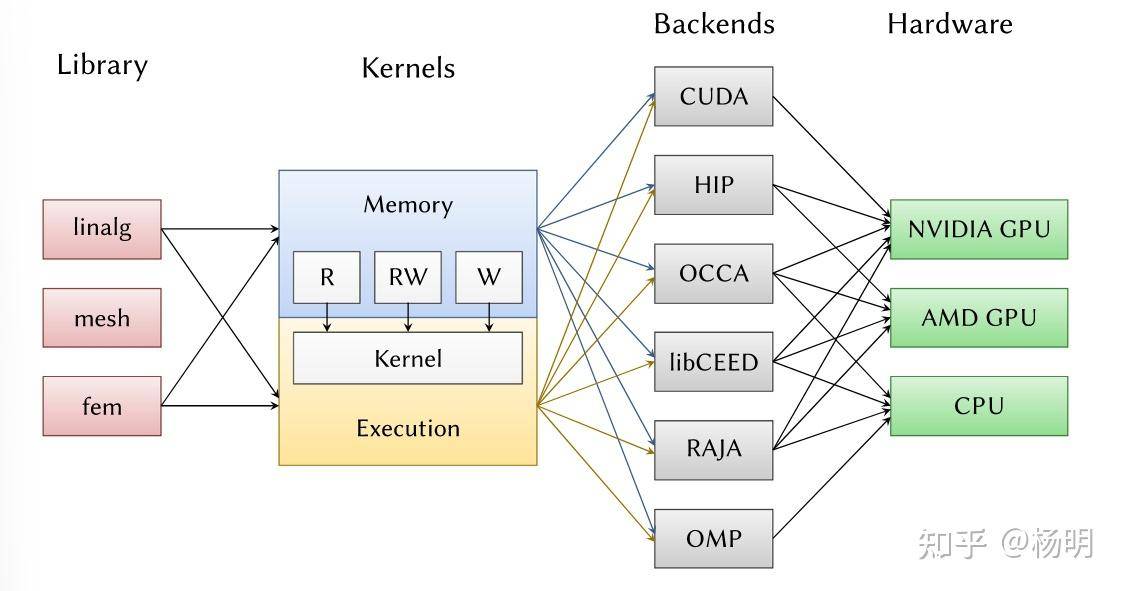
MFEM 支持整个库中的基于 MPI 的并行性，并且可以轻松用作可扩展的非结构化有限元问题生成器。

• 基于 MFEM 的应用程序已扩展到数十万并行核心。
• 库支持张量积高阶元素的有效算子组装/评估。
• 包括对硬件设备（如 GPU）和编程模型（如 CUDA、HIP、OCCA、RAJA 和 OpenMP）的支持。

串行 MFEM 应用程序通常需要最小的更改即可过渡到可扩展的并行版本，它可以利用 hypre 库中集成的可扩展线性求解器。这两个版本可以进一步转换为高性能模板化变体，其中算子组装/评估完全内联特定运行时参数。从 4.0 版本开始，几个示例和许多线性代数和有限元操作的 GPU 加速可用。

内置丰富求解器

MFEM 通常被用作“有限元到线性代数翻译器”，因为它可以将用有限元类型对象描述的问题，转换成相应的线性代数向量和稀疏矩阵。
提供了几种矩阵存储格式，包括密集、压缩稀疏行 (CSR) 和并行压缩稀疏行 (ParCSR)。还支持块向量、算子和矩阵。
对于生成的线性代数系统（或半离散时间积分问题），有多种求解器可用：

• 逐点和多项式串行和并行平滑器，
• 适用于串行和并行通用算子的 Krylov 求解器，例如 PCG、MINRES 和 GMRES，
• 并行特征求解器：LOBPCG 和 AME，
• 来自 hypre 库的高性能预处理器，包括 BoomerAMG、AMS 和 ADS 求解器，
• 来自 PETSc 套件的许多线性和非线性求解器、预处理器和时间积分器，
• 来自 SLEPc 套件的几个特征求解器，
• 来自 Ginkgo 库的多架构（OpenMP、CUDA 和 HIP）上的多种迭代求解器和预处理器。
• 来自 SUNDIALS 套件的 CVODE、ARKODE 和 KINSOL 库的时间积分器和非线性求解器，
• 特定于离散化的求解器，用于电磁、弹性、混合化和 DPG 方法，
• 基于 SuperLU、STRUMPACK 和 SuiteSparse 库的并行和串行稀疏直接求解器，
• 显式和隐式高阶 Runge-Kutta 时间积分器，
• 用于非线性问题（牛顿法、HiOp）和单线性约束二次最小化问题的求解器。

丰富的案例库

MFEM - Finite Element Discretization Library

MFEM提供了40个不同的案例来全面演示了MFEM的使用，这些案例包括固体力学（线弹性问题、弹塑性问题、超弹性问题）、流体力学（可压缩流体、不可压缩流体）、电磁学问题（Maxwell方程组）、不同网格的使用、自适应网格的使用、SubMesh的使用等等。部分案例还同时提供了并行和串行两个版本的代码。许多示例还利用可选的第三方库（如PETSc、SLEPc、SUNDIALS、PUMI、Ginkgo和HiOp）进行了修改。

• 示例 0：最简单的 MFEM 示例，新用户的良好起点（拉普拉斯问题的节点 H1 FEM），
• 示例 1：拉普拉斯问题的节点 H1 FEM，
• 示例 2：线性弹性的矢量有限元，
• 示例 3：确定的 Maxwell 问题的 Nedelec H（curl） FEM，
• 示例 4：用于 grad-div 问题的 Raviart-Thomas H（div） FEM，
• 示例 5：达西问题的混合压力-速度有限元，
• 示例 6：拉普拉斯问题的非一致性自适应网格细化 （AMR），
• 示例 7：表面（单位球体）上的拉普拉斯问题，
• 示例 8：拉普拉斯问题的间断 Petrov-Galerkin （DPG），
• 示例 9：间断 Galerkin （DG） 时间相关平流，
• 示例 10：瞬态隐式非线性弹性，
• 示例 11：并联拉普拉斯特征求解器，
• 示例 12：平行线弹性特征求解器，
• 示例 13：并行 Maxwell 特征求解器，
• 示例 14：拉普拉斯问题的间断伽辽金 （DG），
• 示例 15：具有指定时间相关源的拉普拉斯动态 AMR，
• 示例 16：瞬态非线性热方程，
• 示例 17：用于线弹性的间断伽辽金 （DG），
• 示例 18：欧拉方程的间断伽辽金 （DG），
• 示例 19：不可压缩非线性弹性，
• 示例 20：对称 ODE 积分，
• 示例 21：线性弹性的自适应网格细化，
• 示例 22：复值线性系统，
• 示例 23：时间波动方程中的二阶，
• 示例 24：混合有限元空间和插值器，
• 示例 25：Maxwell 方程的完美匹配层 （PML），
• 示例 26：拉普拉斯问题的多重网格预条件器，
• 示例 27：拉普拉斯问题的边界条件，
• 示例 28：约束和滑动边界条件，
• 示例 29：求解嵌入曲面上的 PDE，
• 示例 30：网格预处理、解析问题数据、
• 示例 31：各向异性定麦克斯韦问题的 Nedelec H（curl） FEM，
• 示例 32：具有各向异性介电常数的并联 Nedelec Maxwell 特征求解器，
• 示例 33：分数拉普拉斯问题的节点 C0 FEM，
• 示例 34：来自 SubMesh 的源函数，
• 示例 35：来自 SubMesh 的端口边界条件，
• 示例 36：障碍物问题的高阶有限元，
• 示例 37：拓扑优化，
• 示例 38：切削面和切削体积积分，
• 示例 39：命名网格属性，
• 示例 40：eikonal 方程。

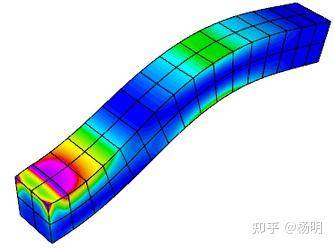
除了这些示例之外，MFEM还提供了许多小程序应用，可以更代表该库在物理 / 应用程序代码中的高级用法。一些包含的小程序包括：

• Volta：简单的静电仿真代码，
• Tesla：简单的静磁仿真代码，
• Maxwell：瞬态电磁仿真代码
• Joule：瞬态磁学和焦耳热小程序，
• Navier：不可压缩瞬态 Navier-Stokes 方程的求解器，
• Mesh Explorer：可视化和操作网格，
• Mesh Optimizer：优化高阶网格，
• Mesh Fitting：优化网格以符合离散水平集的零等值面，
• Mesh Quality：可视化和检查网格质量，
• Interpolation：物理空间中高阶有限元函数的评估，
• Overlapping Grids：单物理场和多物理场问题的 Schwarz 耦合，
• Extrapolation：有限元外推求解器，
• Distance：有限元距离求解器，
• Shifted Diffusion：非体拟合网格的高阶 Shifted 边界方法，
• Minimal Surface：计算给定网格的最小表面，
• Display Basis：可视化有限元基函数，
• Get Values：通过 DataCollection 类提取字段值，
• Load DC：可视化通过 DataCollection 类保存的字段，
• Convert DC：在不同 DataCollection 格式之间进行转换，
• LOR Transfer：在高阶和低阶细化空间之间映射函数，
• ParELAG H(curl) and H(div) AMGe：使用 ParELAG 库中基于元素的代数多重网格 （AMGe） 求解 H（curl） 和 H（div） 问题。
• SPDE：通过 SPDE 方法生成高斯随机场;即，通过求解具有随机载荷的分数式偏微分方程，
• Contact：使用 Tribol 库进行砂浆接触斑贴试验的弹性，
• Multidomain：Multidomain 和 SubMesh 演示小程序，
• DPG：非间断 Petrov-Galerkin （DPG） 的各种示例。

此外，MFEM还提供了基于 MFEM 构建的几个外部基准测试/代理应用程序的源代码：

• Laghos：高阶拉格朗日流体动力学小程序，

Center for Efficient Exascale Discretizations

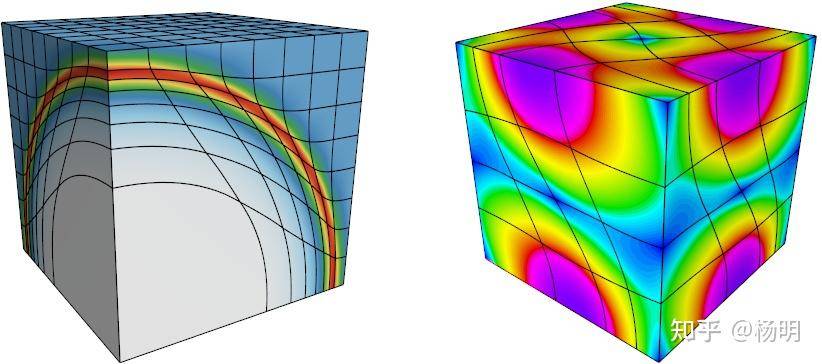
• Remhos：高阶平流重映射小程序，

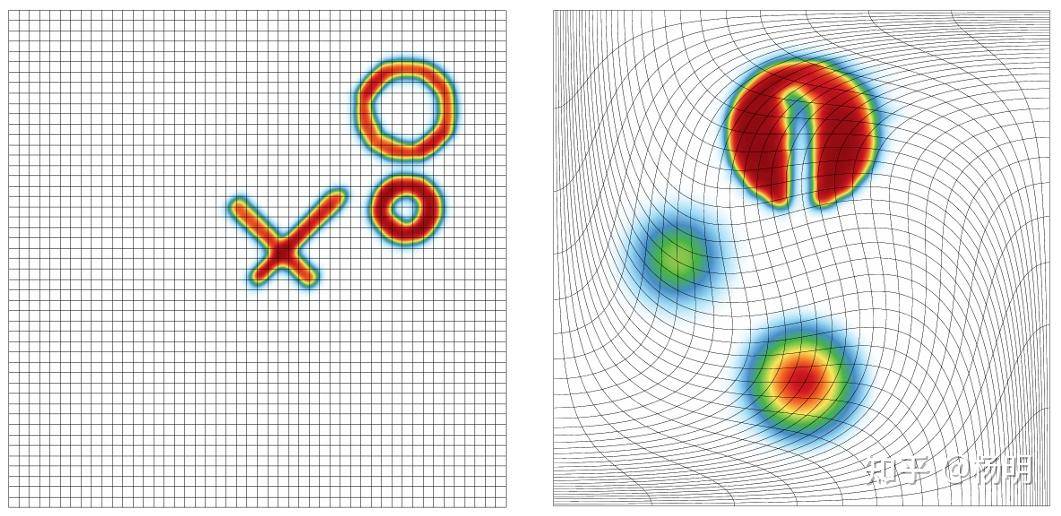
• Mulard：多组热辐射扩散微型应用。

AMG2013

MFEM另外提供了一些不太严肃的 “玩具” 迷你应用程序展示了 MFEM 的灵活性（并提供了一点乐趣）：

• Automata：简单元胞自动机的模型，
• Life：康威(Conway)人生游戏的模型，
• Lissajous：旋转的视错觉，
• Mandel：使用 AMR 进行分形可视化，
• Mondrian：将任何图像转换为 AMR 网格，
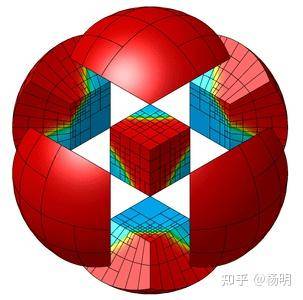
• Rubik：互动魔方™拼图，
• Snake：魔方™蛇拼图的模型。

可视化

• MFEM 中的通用（高阶）网格和有限元函数可以使用配套的 OpenGL 可视化工具 GLVis 精确地可视化，该工具建立在 MFEM 的基础之上。
• VisIt 可视化和分析工具也原生支持 MFEM 格式。
• MFEM 原生支持的另一种可视化工具是 ParaView。该文件格式支持高阶（最高六阶）网格和单元。

MFEM新功能

GPU 和 HPC 功能的进展

1. 高阶有限元的无矩阵求解器

传统上，高阶有限元问题常通过迭代方法和有效的预条件器求解。然而，不仅高性能的预条件器的构造和应用殊为困难，与离散化相关矩阵的组装和存储更是代价高昂（在内存占用和计算复杂度方面）。在这种情况下，传统基于矩阵的方法不能充分利用GPU提供的计算资源。
无矩阵预处理方法，适用于各种有限元算子和离散化。这样的预条件器可以在不访问组装矩阵的情况下构造和应用，并且它们的内存使用是渐近最优的（与问题大小线性缩放）。MFEM 主要支持两种：p-multigrid 和 low-order-refined preconditioning。
在p-multigrid中，构建了一个具有不同多项式度数的有限元空间层次结构，这些空间在同一网格上是嵌套的。这种嵌套性质允许构建限制和扩展算子，这些算子在不同度数的空间之间传递解和残差。使用仅基于矩阵对角线的平滑器和GPU上的因式分解技术提供了无需组装矩阵即可有效计算有限元矩阵对角线的算法。
Low-order-refined (LOR) preconditioning也称为SEM-FEM预处理，基于在细化版本的网格上构建一个在谱上等价的最低阶离散化的思想。即，高阶离散化在原始网格上，低阶离散化在细化网格上，两者具有相同数量的自由度。在某些网格构造条件下，这两种离散化是谱等价的，与网格大小和多项式阶数无关。因此，使用低阶矩阵构建的预处理器可以有效地预处理高阶算子。

2. 在百万兆平台和AMD GPU上实现先进性能

为支持在一系列基于GPU的平台的高性能计算，MFEM支持四种组装级别，各有不同的计算效率和内存使用属性。

• 完全无矩阵：所有数据动态计算，最小化存储和内存要求，有可能潜在的重复计算的开销。
• 部分组装：仅预先计算和存储正交点处的基本数据，与完全无矩阵相比，降低了计算成本，同时与矩阵汇编相比减少了内存占用。部分组装对于高阶有限元特别有效。
• 单元组装：计算每个单元的局部贡献并将其存储在单元局部密集矩阵中。虽然这种方法比部分组装更耗费计算和内存，但它也允许访问运算符的代数表示。
• 稀疏矩阵组装：传统的组装方法，计算并存储表示运算符的全局稀疏矩阵。虽然这对于大规模问题（尤其是高阶有限元）来说可能是内存密集型的，但它与各种现有的求解器和预条件器兼容。

MFEM 中的所有上述装配级别都旨在与基于 GPU 的执行兼容，利用现代 GPU 的计算能力来加速仿真。与 GPU 上的设备执行的兼容性使 MFEM 能够更高效地处理复杂的大规模问题，使其成为科学计算和工程模拟的多功能工具。

MFEM 扩展了其功能，以完全支持百万兆次级计算平台，包括对多个 GPU 架构的优化支持。另外，MFEM 无矩阵内核在 NVIDIA 和 AMD 架构之间也显示出良好的性能可移植性。

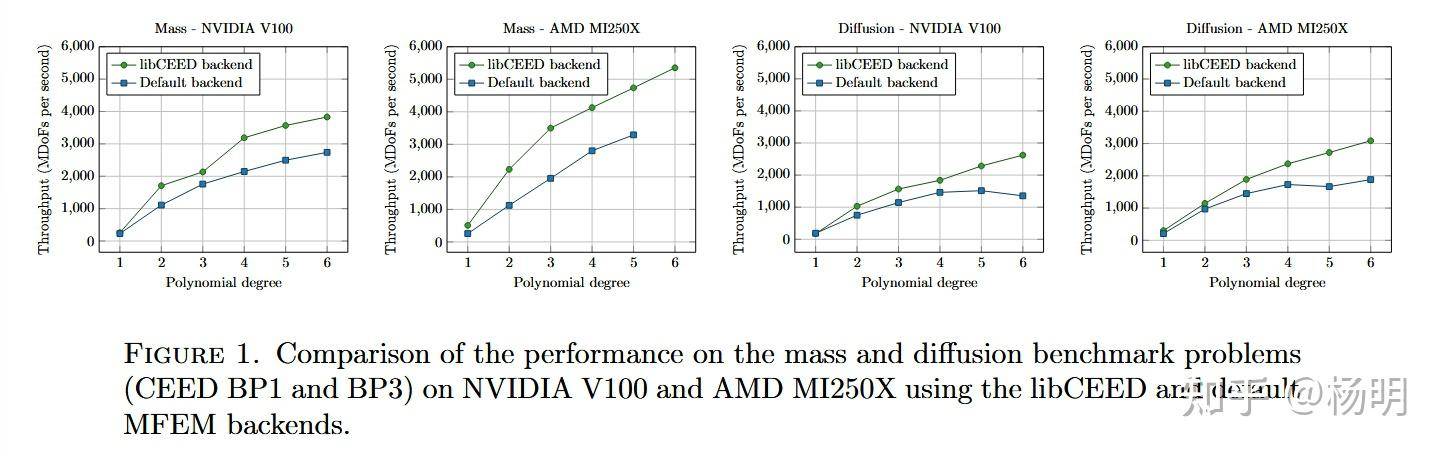
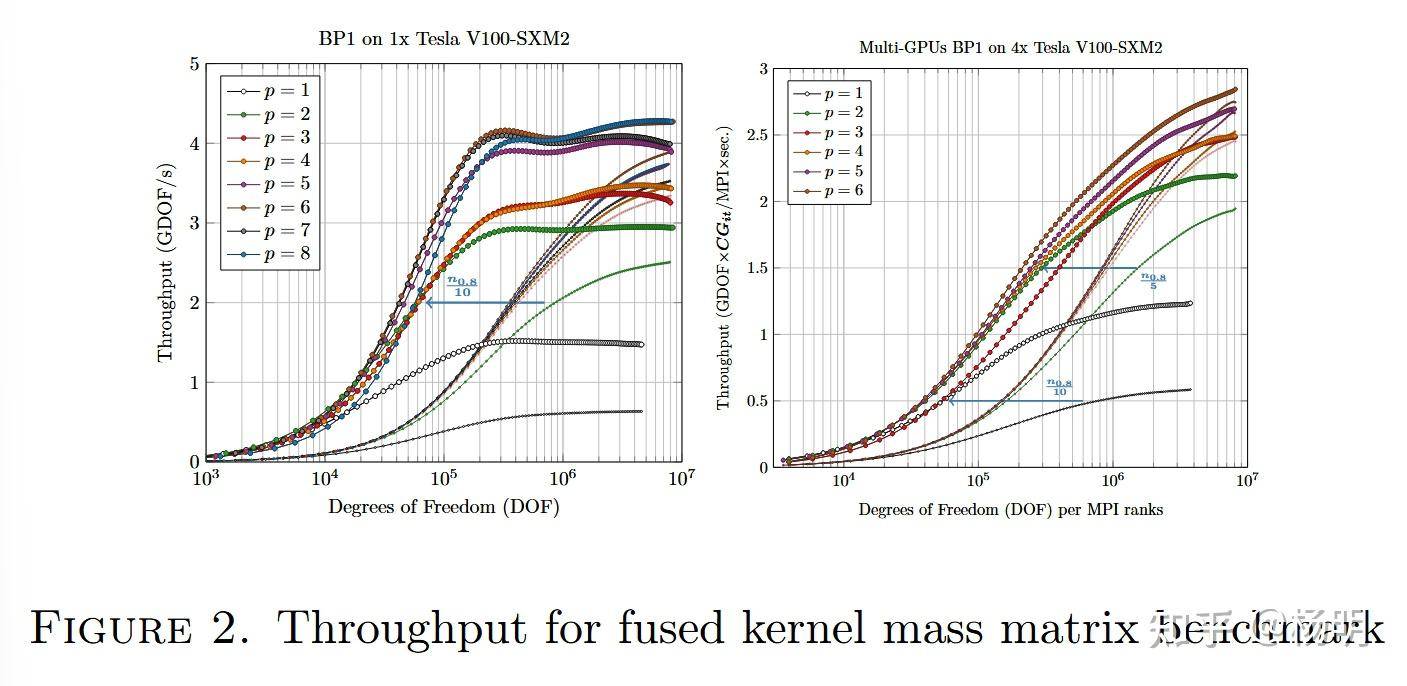
3. 内核融合

GPU 内核融合是最大限度地提高 GPU 加速有限元选项的性能和可扩展性的重要技术。它的挑战之一是提供用户友好的编程接口来生成融合计算内核。
内核融合的实现涉及到多个层面的优化，MFEM团队利用UFL语言进行抽象，通过在编译器前端级别构建的模块化工具链将 UFL 转换为 C++ 和原始 CUDA，进而实现静态分析和优化。
为了实现CEED基准问题，需要多个构建块，包括不同拓扑的内核启动、特定warp级别的指令以及同步不同算法部分的机制。这部分在 Nvidia GPU 上的实现是通过使用合作组Cooperative Groups编程模型，即使用组分区进行组织，并使用组集体进行同步。

4. 混合网格、非协调网格和p-自适应

• 非协调网格上的无矩阵DG方法，建立在先前实现的协调无矩阵DG方法的基础上。这一实现的一个关键方面是有效处理非协调面，通过变换自由度来实现，这允许在非协调网格上使用标准的协调面内核。这种非协调变换仅在非协调面上的E-vector级别发生，最小化了其计算成本。对于非协调面，自由度从粗面插值到细面，使得从计算的角度来看，面看起来像是协调面。
• libCEED库的集成为MFEM的无矩阵算子增添了独特的功能，包括对不同几何类型的单元（包括简单形、金字塔和楔形）的支持，以及p-自适应（多项式阶数）。MFEM用户可以通过简单地使用libCEED后端，在混合网格和p-自适应上运行模拟，使用无矩阵算子。

离散化支持的进展

1. DPG方法

MFEM现在支持de Rham complex上的大量DPG模拟，提供了用户友好的类允许用户自定义试函数和权函数及其上的线性/双线性积分器。非常适合解决容易丧失离散稳定性的问题（如高频时谐声学和电磁方程）和需要自适应网格细化 (AMR) 的难题（如奇异解问题）。

2. Proximal Galerkin方法

Proximal Galerkin方法是一种用于处理具有点wise约束的偏微分方程（PDEs）的高阶非线性数值方法。MFEM现在通过两个新示例提供了PG方法的实现，即ex36和ex37。

3. 浸入式离散化

MFEM库中添加了对浸入式网格上有限元计算的能力。这些方法假设感兴趣的特征（域边界或内部界面）由离散函数的零水平集隐式给出。新特性的共同目标是：在避免纯几何计算的同时，坚持有限元操作。这一原则使得跨维度、单元阶数和有限元离散化类型的泛化性更好。
在切割单元上的积分。MFEM提供了两种替代方法来构建离散预设切割面和体积上的积分规则。第一种方法依赖于外部Algoim包，它通过执行降维来构造1D积分规则的组合，适用于矩形和六面体单元。第二种方法使用了在文献Highly accurate surface and volume integration on implicit domains by means of moment-fitting中介绍的矩匹配算法。这种方法为每个单元构造了一组基函数，以定义和解决局部欠定系统的积分权重向量。形成系统所需的所有表面和体积积分都简化为对相交段的1D积分，新开发的积分技术允许快速有效地实现高阶CutFEM离散化。
移位边界方法。MFEM还提供了移位边界方法（SBM）的实现，这是一种避免在切割单元中积分的技术，而是使用替代的计算域。该方法使用到真实边界的距离函数在（非对齐的）替代网格面上强制执行所需的边界条件，从而将施加边界条件的位置“移位”。
距离和外推求解器。在涉及水平集函数的计算中，通常需要离散距离求解器。MFEM的Distance miniapp展示了计算从给定点源到计算网格中的最短路径或给定函数的零水平集的能力。

4. NURBS patches上的部分组装

除了对单元的部分组装支持之外，MFEM现在还支持在NURBS patches上进行部分组装，这在等几何分析的设置中非常有用。当在patches级别而不是单元级别上进行组装时，可以节省显著的计算资源，因为整个patches的单元存在张量积结构，这允许在求和因子分解中获得更多的利益。从这个意义上说，包含许多单元的NURBS patch可以被视为一个非常高阶的单个单元。

5. 自动微分

一个协作努力，即 ∂FEM 项目，旨在集成 Enzyme 工具并进一步开发基于运算符重载和模板的原生 MFEM AD 实现，以满足在 FEM 离散化和最优设计应用中自动计算残差、雅可比矩阵和 Hessian 矩阵的需求。
与在全局级别应用自动微分的传统工具不同，MFEM 的有限元算子分解允许在最内层的积分点级别处理导数。算子将数据从全局级别转移到子域、单元和积分点级别，即 P、G 和 B，它们是线性和拓扑的：它们不依赖于解、物理坐标或设计参数。因此，它们可以从微分循环中排除，节省大量内存和计算。分解将代码修改限制在积分点级别，允许对复杂非线性问题完全自动化离散化过程。
∂FEM 工作仍在进行中。

网格划分功能的进展

1. 高阶网格优化

MFEM中的高阶网格优化框架基于目标矩阵优化范式（TMOP）。适用于所有单元类型（二维和三维中的四边形、六面体、简单形、金字塔），支持 h/p-细化网格，并且可以利用针对 GPU 加速的有限元组装技术。这方面的最新成果如下：

• 开发了用于不同网格自适应目标的自动目标构造方法。对于一般网格质量改进，基于理想单元类型（例如立方体或规则四面体）设置目标几何属性。对于模拟驱动的优化，使用离散解或派生量（例如误差估计）来设置目标几何属性。
• 研究了不同网格质量度量的理论属性，以识别不同类型的良置度量。开发了新的渐近平衡复合度量，这些度量在预设的 λ 范围内平衡，无需用户干预。还开发了新的网格质量度量，可以同时解开网格并改善最差的单元质量。这些度量对于处理严重或局部网格畸变的问题至关重要。
• 向TMOP增加了惩罚项，以弱化所选网格节点集与隐含曲面的对齐，同时优化网格质量。另外，使用 MFEM 的 p 自适应性框架进一步增强了这个公式，以获得混合阶网格，这样高阶单元只在目标表面的高曲率区域附近使用。与常序网格相比，这种 rp 自适应性方法已被证明可以以较低的计算成本获得具有相同几何精度的混合阶网格 。
• 最后，为了支持利用 GPU 的 MFEM 基础应用，MFEM团队实现了与 TMOP 相关的算子，采用求和因子分解和部分组装。这包括评估 TMOP 目标函数及其一阶和二阶导数的新 GPU 内核，以及加速牛顿求解的雅可比预处理器。在 GPU 上使用求和因子分解和部分组装，与在 CPU 上使用传统完全组装矩阵技术相比，显著减少了牛顿求解的时间。

2. 子网格接口

MFEM最近新增了子网格接口，它允许应用程序定义一个代表父网格子集的网格。子集可以由体积单元或边界单元形成，分别创建域或表面网格。子网格是一个完全功能的MFEM网格，因此可以利用MFEM现有的所有机制在单个或多个子网格上进行操作。此外，MFEM提供了在父网格与其子网格之间或共享同一父网格的子网格之间传输网格函数的能力。
通过子网格接口，用户可以在复杂的多域问题中更灵活地定义和操作网格，实现不同物理过程的耦合和数据交换。

暂未实现/还在开发中的功能

• 目前 MFEM 不支持 NURBS 网格的并行细化。
• 上文提到的高阶矩阵部分组装算法，目前在张量积单元（即四边形、六面体）中实现，而单纯形单元（三角形和四面体）的部分组装还在规划中。
• MFEM 库中的许多功能仍未移植到GPU上，包括网格细化/去细化、一些 BilinearFormIntegrator 类、稀疏矩阵组装、误差估计、与外部库的集成等。其中一些缺失部分目前正在开发中，不久的将来就会可用。
• 将 MFEM 的网格优化能力扩展到仿真驱动的自适应性（又名 r 自适应性），以及通过结合TMOP和AMR概念耦合高阶网格的 h 和 r 自适应性的工作正在进行中。
• ∂FEM 项目，旨在集成 Enzyme 工具并进一步开发基于运算符重载和模板的原生 MFEM AD 实现，以满足在 FEM 离散化和最优设计应用中自动计算残差、雅可比矩阵和 Hessian 矩阵的需求。该工作正在进行中。

写在最后

感谢你阅读，期待你点赞、收藏和关注，支持原创。整理不易，如有谬误，请大家及时指正！感兴趣的可以加入MFEM中文社区，共享开发经验：

Q群：760401312

Wechat ID: ym_cae（备注MFEM社群）