有哪些算法惊艳到了你？
要论最让我惊艳的算法，莫过于博弈论中的无偏博弈问题的算法。让我们从一个简单的游戏：Nim Game来了解无偏博弈问题与其令人惊叹的简单算法。
Nim Game
什么是Nim Game
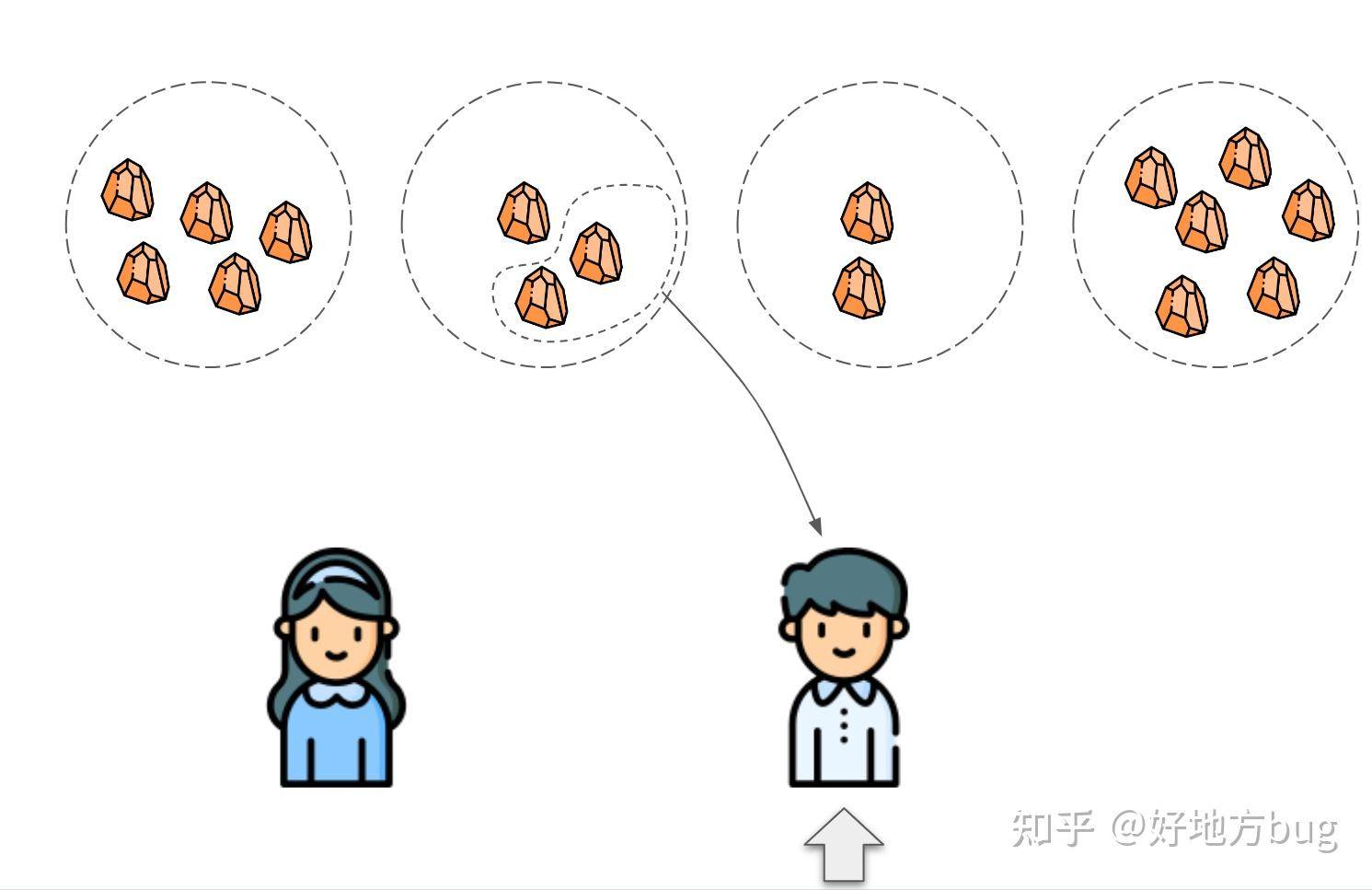
考虑现在有两个绝顶聪明的人：丧彪和小美。他们决定玩一个游戏：
- 丧彪和小美面前有
堆石头
- 第
- 每人每轮需要任选一堆石头，从中取走大于0个石头
- 谁没有石头可以拿，便输了（即上一轮对手拿完了所有石头，或者一开始就没有石头）
- 丧彪先走
现在请问，给定石堆数量 与每堆石头的数量
，丧彪和小美在采取绝对最优的策略下，谁会胜出。
让我们思考一下
为了解决这个问题，我们不妨从一些简单的初始情况来讨论。
| 局面 | 丧彪（先手） | 小美（后手） | 策略 |
|---|---|---|---|
| 开局压根就没有石头 | 输 | 赢 | 小美躺赢 |
| 开局只有一堆石头 | 赢 | 输 | 丧彪先手拿完，小美便没有石头可拿 |
| 开局有两堆石头，但是两堆石头数量一样 | 输 | 赢 | 小美只需要做丧彪的对称动作，例如丧彪在其中一堆里面拿 x 个石头，小美只需要在另一堆同样拿 x 个石头。那最后一定是丧彪没有石头可拿。 |
| 开局有两堆石头，但是两堆石头数量不一样 | 赢 | 输 | 这时候，丧彪只需要瞄准多的那一堆，把多余的石头拿走，使得两堆一样，就回到了上面的局面，但换做了小美先手。所以这种情况下丧彪赢。 |
显然，我们有废话：每个局面，不是先手胜，就是先手败。
观察上面第4个开局，这种局面下，丧彪发现能将局面转换为一个小美先手，但是小美必败的局面，所以丧彪开局必赢。
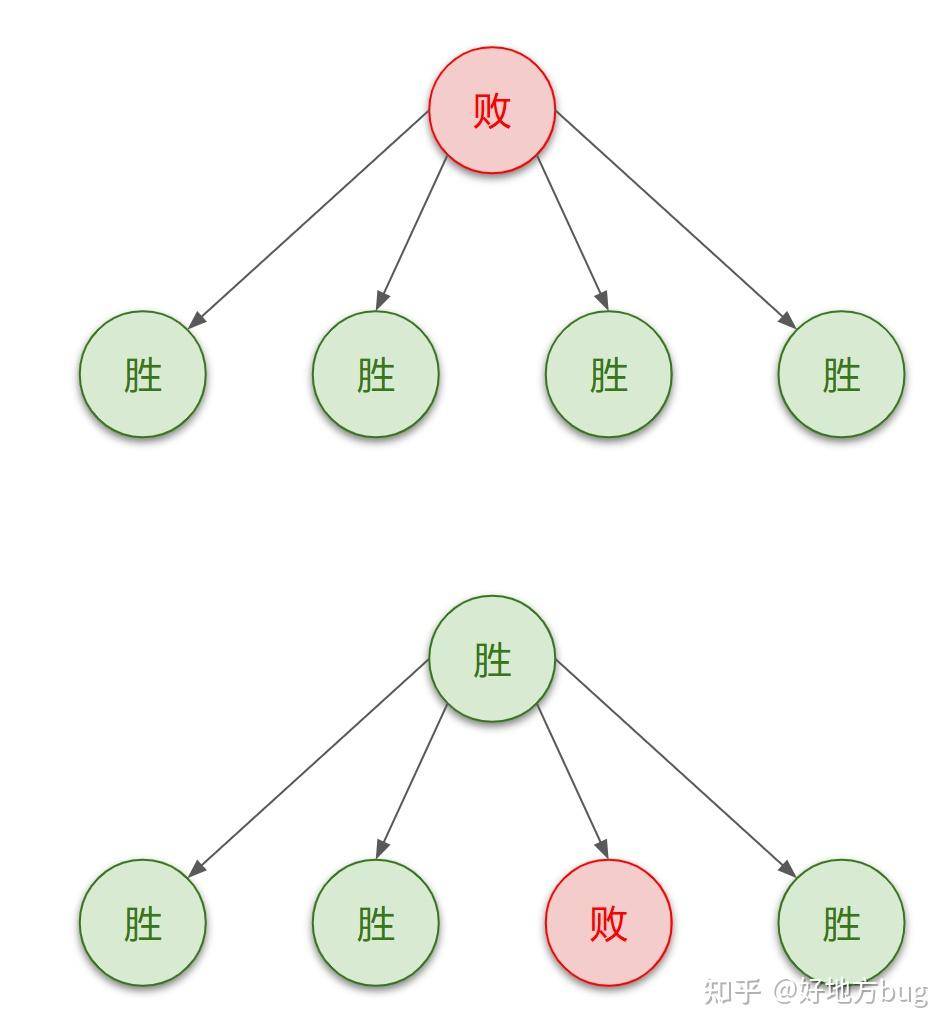
所以如果一个局面：
- 没有后继局面（例如面前没有石子），那么先手败；
- 所有可能的后继局面都是先手胜，那么当前局面先手败；
- 而如果一个局面的后继局面中，有先手败，则当前局面先手胜。
注意，上述对于先手胜败的论断，对后续的分析十分重要，大家伙记住了奥。
搜索策略
熟悉搜索的小伙伴已经快掏出自己的深度优先搜索跃跃欲试了。没错，此时搜索已经完全能解决丧彪赢还是输的问题。
我们不难得到一个非常暴力的搜索，只需要递归考察每个后继局面是必胜还是必败：
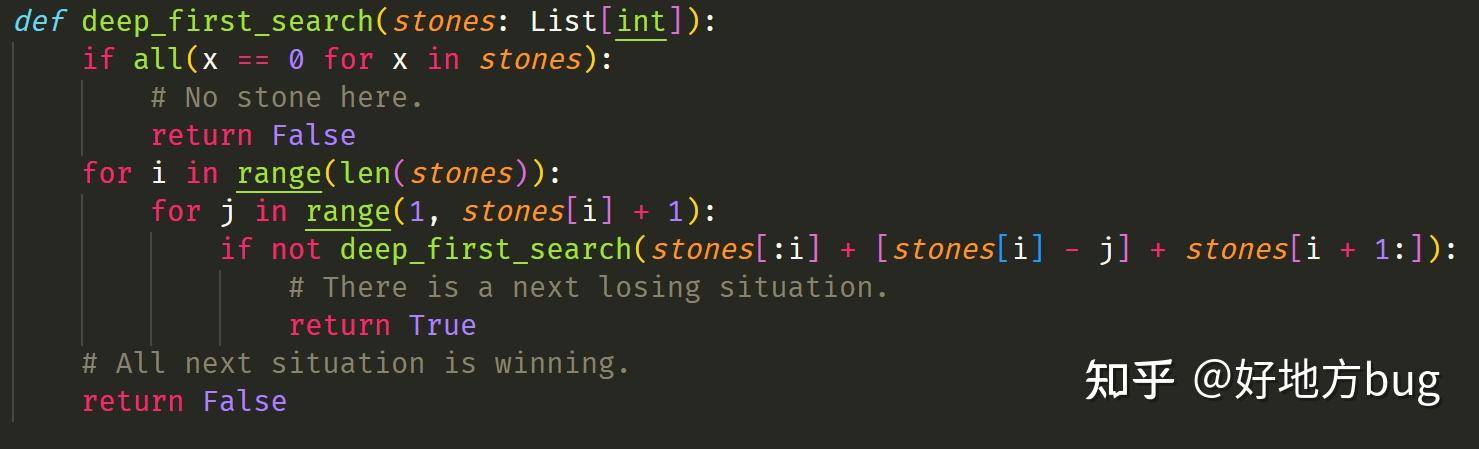
嗯，很好。我们拿来实验一下。
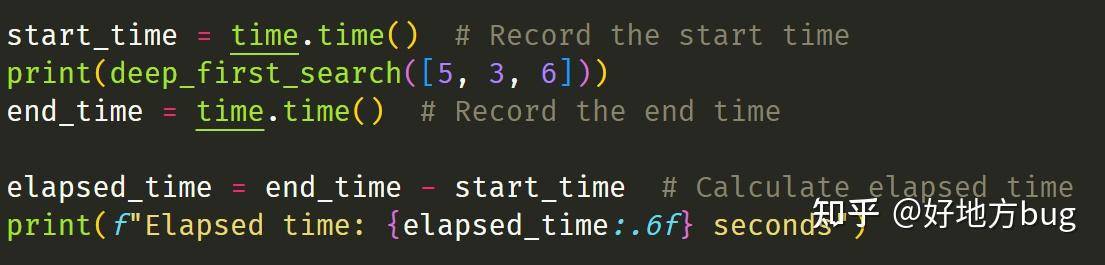
光是计算5，3，6这个简单的开局就用了接近2秒。
而计算5，3，6，2这个局面，就更困难了：
有小伙伴一定会意识到一个问题，我们在搜索的时候一定有很多重复的局面。例如对于5，3，6这个局面，我先搜索第一堆取2个，第二堆再取1个。和我先搜索第二堆取1个，第一堆再取2个。是一样的。
所以我们可以优化一下，例如通过哈希（这里我们用一种简单的质数哈希的办法），记忆每个局面，搜过了就不用再搜了。
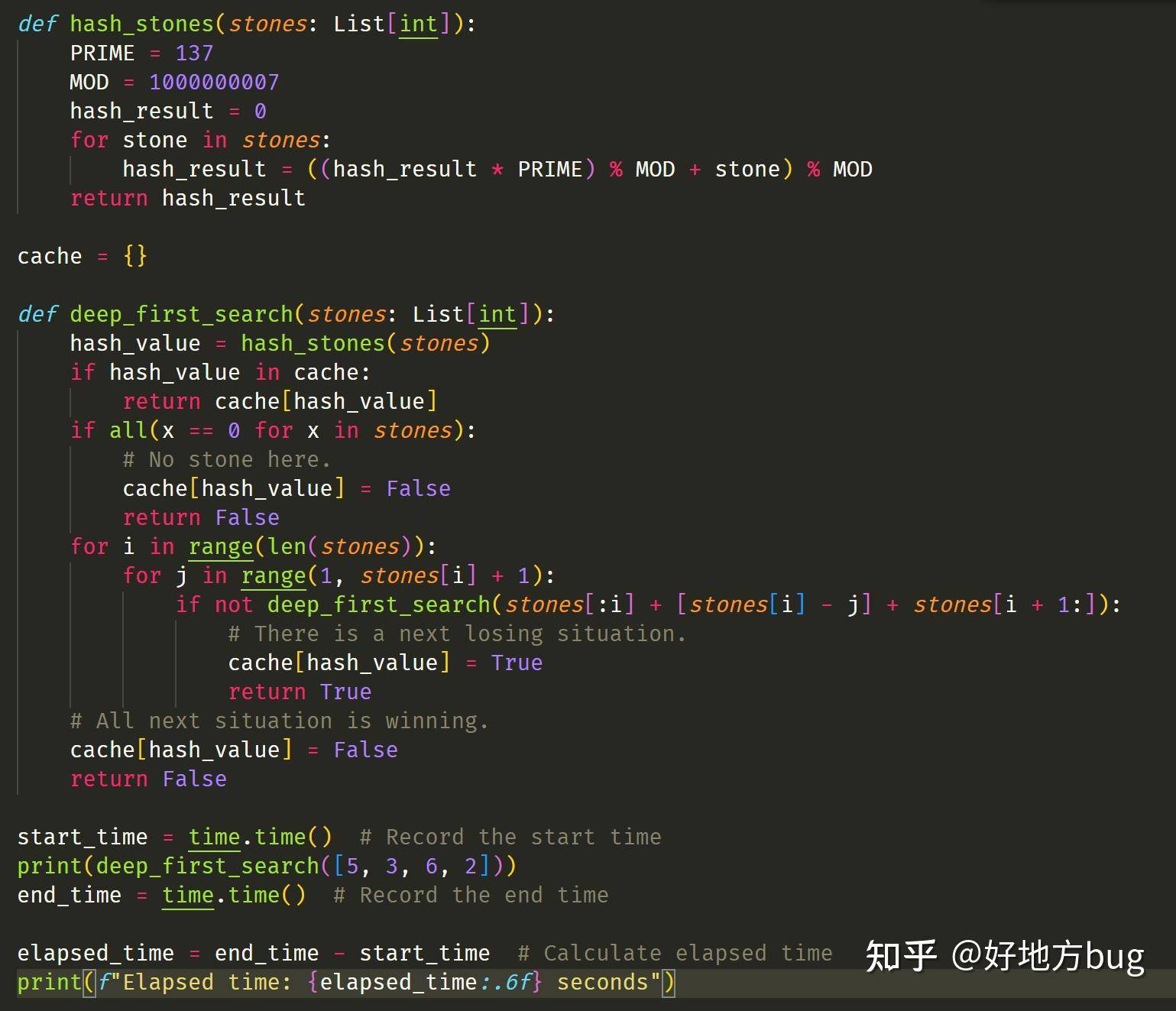
嗯快了好多！！但是这就是我们想要的解决方案了吗？我们不妨分析一下复杂度：
每个石头都有可能减少任意数值，所以总的局面数是 。所以复杂度是
。当
相当大的时候，或者只要
稍稍一多，复杂度不可避免爆炸！
想必绝顶聪明的丧彪和小美，脑袋里也不会跑这种，等到大道都磨灭了，都算不出来的算法。
按位异或
我们回顾一下上面的搜索，搜索本身是在刻画我们对先手胜败的论断，而我们对搜索的优化，本质上是在对局面进行编码计算。
那有没有办法把这两者结合一下呢？即，我们能找到一种对局面的计算，使得能够刻画我们先前提到的关于先手胜败的论断。
而这个计算就是：按位异或（bitwise-xor），我们用 来表示。
什么是异或：异或是简单的0 1计算规则满足：
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
即相同则返回0，不同则返回1。
什么是按位异或：对于两个 位（不足
就补
）二进制数，
和
。我们定义
和
的按位异或为
。也即每一位依次异或。例如
，则
。
按位异或有什么性质：注意到0 xor 0 = 0 且 1 xor 1 = 0，所以如果 则
；类似的，
。
这里我们给出这个神奇的定理。
定理：对于 堆石堆的Nim Game，若每堆石头的数量为
，则先手必胜当且仅当
。
证明：
我们通过验证按位异或是否满足我们前面对先手胜败的论断，来证明上述定理。
Case 1:
若场面上没有石头，即， ，则
，先手败。
Case 2:
若 ，且
。我们修改任意一个 ，使得其值降低。则接下来的按位异或和必不等于0，同时也是一个合法的Nim Game行动（这是由于我们是在降低值）。即后继局面中，不可能还存在使得按位异或和还等于0的情况，即后继局面都是必胜的。所以当前局面必败。
Case 3:
若 ，则我们考虑
的二进制。其一定有一位是
。我们把
最高位的
给拿出来，这个
一定来自于某个
（总不能凭空产生一个
吧）。接下来，我们把
中所有对应在
中是
的位置全部翻转（这句话有点长，注意是翻转
）。这会导致两个结果：
- 整个按位异或和变成了
这意味着，第一，这是一步合法的Nim Game操作；第二，后继局面里存在按位异或和为 的局面，即后继局面里面有必败的局面。
故当前局面能通过一步合法操作，使得后继局面必败。故当前局面先手必胜。
QED
注意：咱们这里的证明实际上是个归纳证明，即假设更小的局面总是满足定理的。
利用这个性质，我们再重新设计算法就非常简单了：
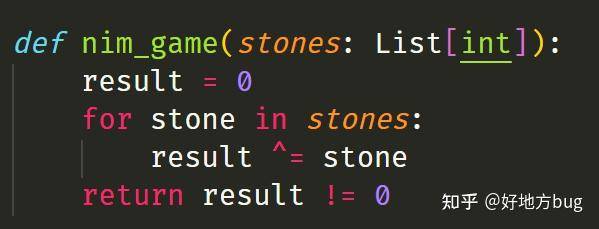
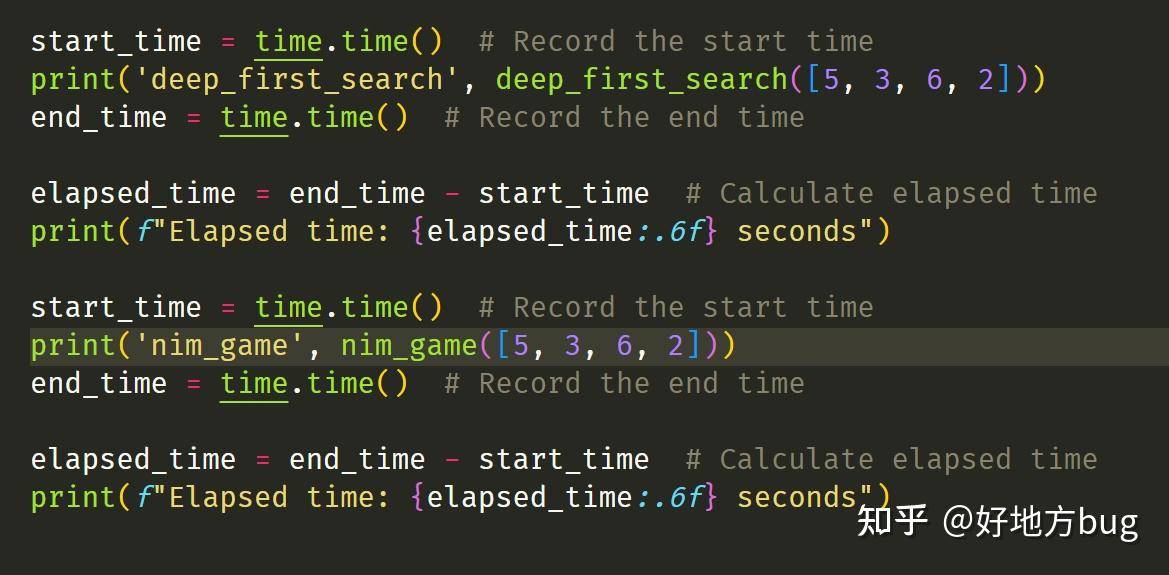
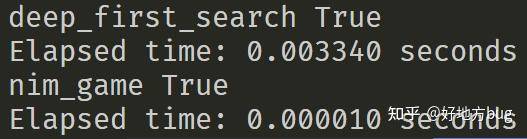
可以看到，同样计算[5, 3, 6, 2]，我们利用异或和，要快很多很多。这时我们的复杂度来到了 。
无偏博弈
现在我们来考虑更一般的无偏博弈问题。
什么是无偏博弈
类似Nim Game，无偏博弈（Impartial Game）需满足如下条件：
- 两个游戏者轮流执行步骤；
- 当有玩家不能动的时候，即无可执行的步骤时，游戏结束，并选出胜者；
- 局面和操作必须是有限的；
- 两个游戏者除开先后手外，没有任何区别；
- 完全信息，所有游戏者都能看到整个局势；
- 无随机行动。所有行动都确定性地将目前局势转变到下一个局势。
例如我们常见的象棋围棋等，就不是无偏博弈，因为双方除开先后手区别，所持有的棋子也不一样。
另外像麻将，扑克等桥牌也不是，因为不是完全信息，每个游戏者不能看清整个局势。
那除开Nim Game，有什么其他游戏是无偏博弈的呢？这里给出一些例子。
Chomp：一块 的巧克力板，左上角那块有毒。丧彪和小美轮流选一块巧克力，选择之后，需要吃掉这块以及其右下方的所有剩余巧克力。谁吃掉有毒那块，谁就输了：
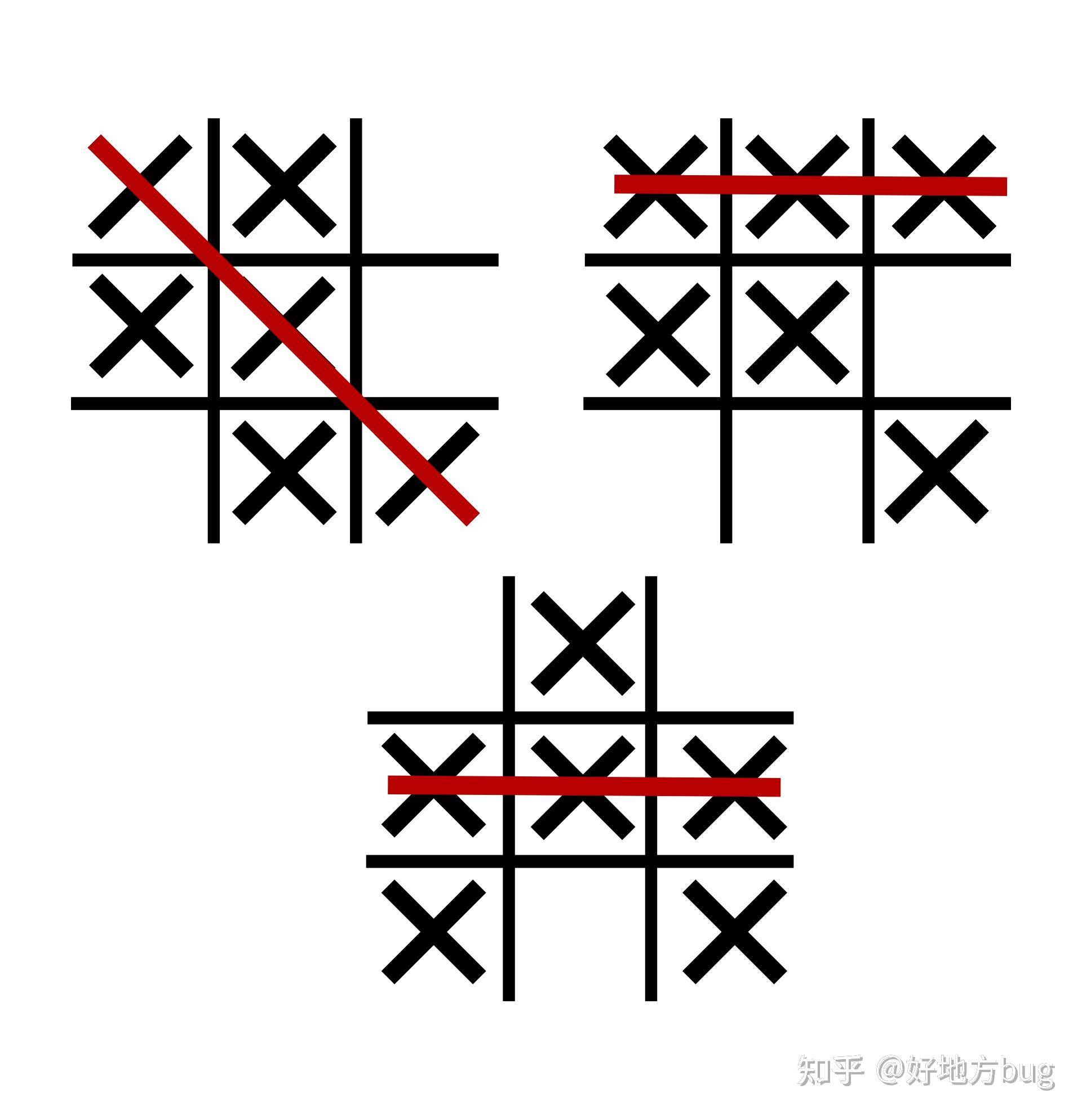
Notakto：Notakto是井字棋的变种。考虑有 个井字棋棋盘，丧彪和小美都使用
来作为棋子。每人每轮可以再任意一个还没结束的井字棋棋盘里面下一个
，当一个井字棋棋盘中出现三连，则此棋盘结束。当没有井字棋棋盘可以下子的时候，输掉。
无偏博弈的组合游戏：是的没错，无偏博弈的组合依然是无偏博弈。例如我们可以同时玩Nim Game和Notakto。丧彪和小美，每轮可以选择去拿Nim Game里面的石头，或者是填Notakto里面的井字棋。谁没有操作可以做了，谁就输了。
那这种更一般的无偏博弈问题，我们该如何解决呢？
Sprague–Grundy 定理
类似我们在Nim Game中的处理，我们需要一个指标，来刻画当前局面的输赢。
我们定义函数 为集合
中最小的没有出现过的自然数，即：
例如 ，
。
接下来，我们定义一个函数
对于一个单局游戏（例如Nim Game中的一堆石头，或者Notakto中的一个井字棋）的状态 ：
- 若其无后继局面，即无路可走的必输局面，则
- 若其后继局面为
Sprague–Grundy 定理：对于一个有 个单独游戏组合而成的局面
，若其每个游戏的状态为
，则局面
的
值为：
。且局面
先手必胜当且仅当
。
有点绕是不是？我们举些例子：
比较容易观察到，对于Nim Game而言，每一堆石头的 函数应当等于这堆石头本身的数量，例如下图所示：
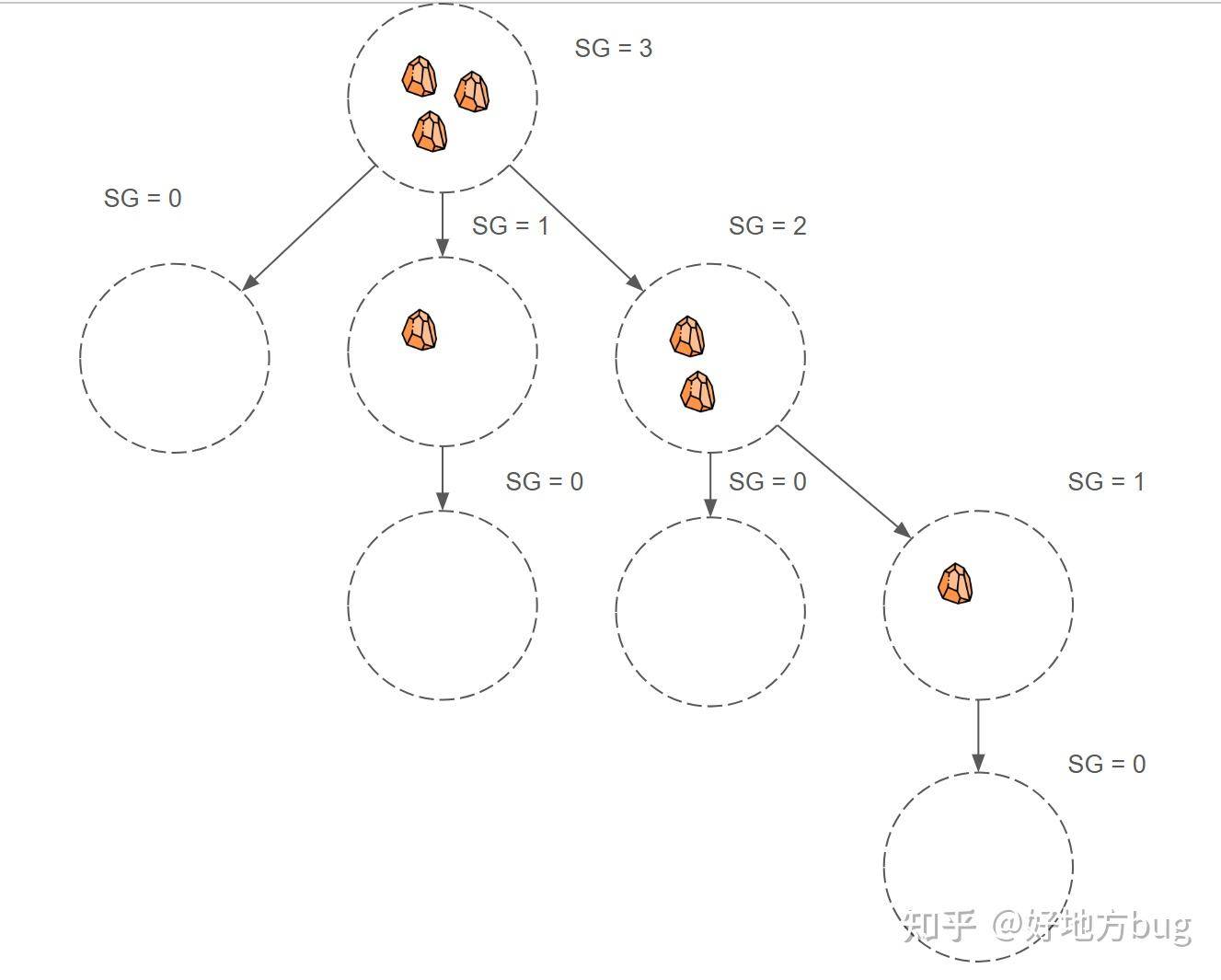
我们再给出一个Notakto的例子：
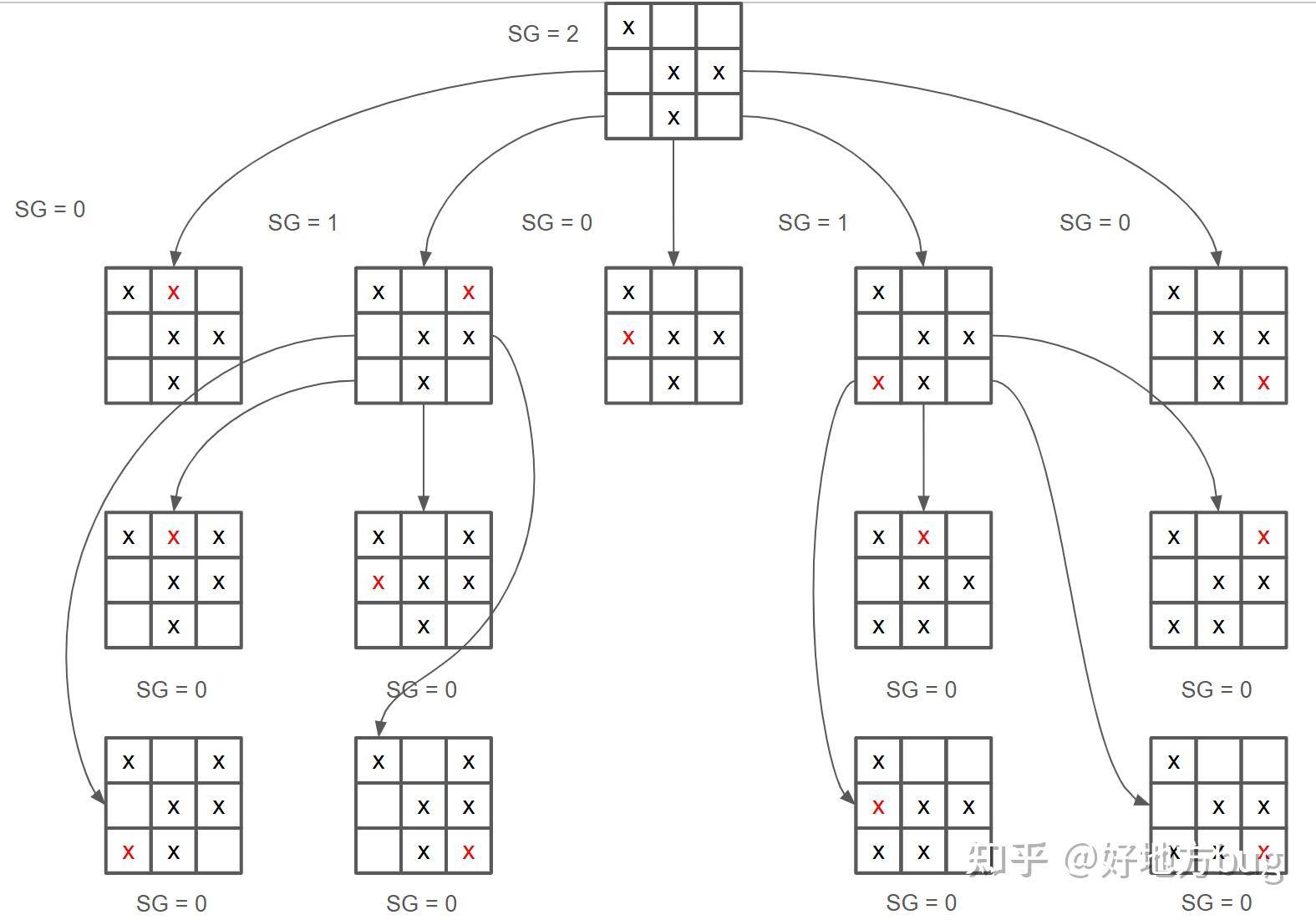
对于组合的游戏：
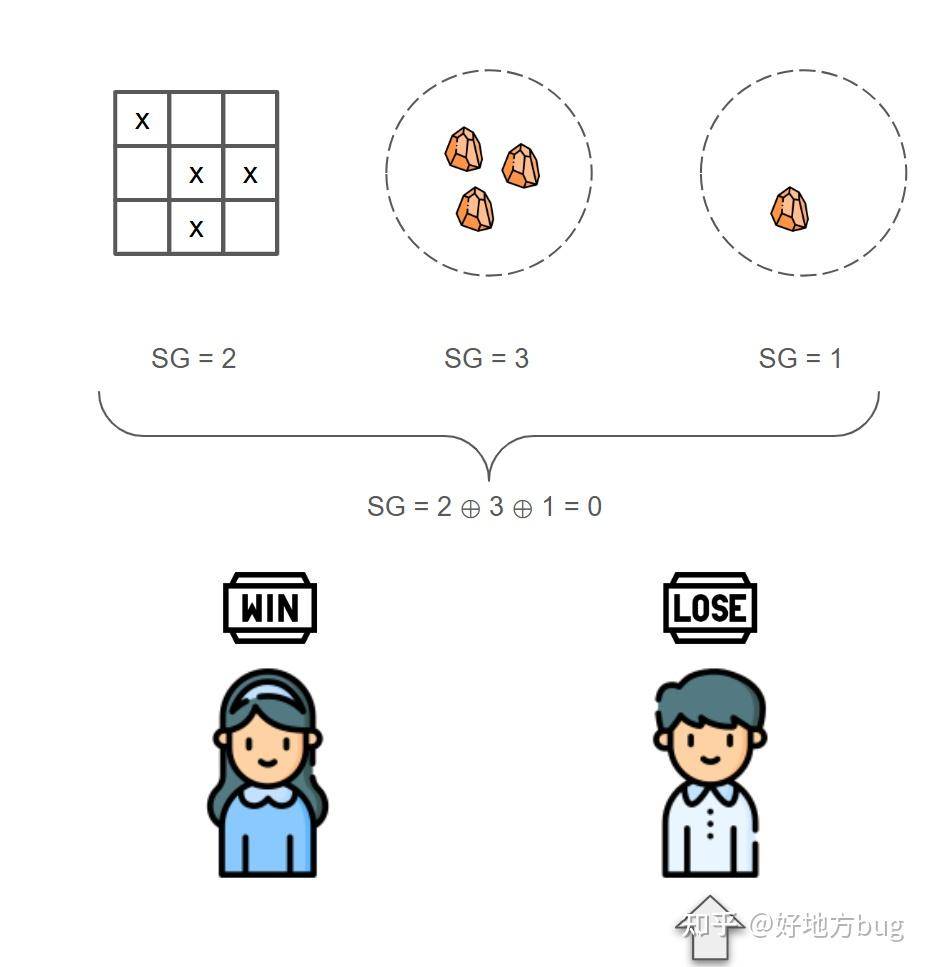
证明这里就不详细展开了，可以留作小伙伴们自己思考，聪明的小伙伴可以在评论区留下自己的想法。这里给出一些提示：
SG函数的构造，使得任何一个无偏博弈问题，可以转换为一个Nim Game
算法
依靠Sprague–Grundy 定理，判定一个无偏博弈问题是否为先手必胜，我们只需要：
- 找到每个单独游戏的后继状态集合
- 递归，用mex函数计算每个单独游戏的SG值
- 若当前局面为若干个独立的单独游戏的组合，则利用按位异或计算SG值
- 最终计算出初始局面的SG值，若其大于0，则先手必胜，否则先手必败。
写在后面
Nim Game的巧妙在于其通过引入二进制按位异或，来解决一个看起来和二进制毫无关系的问题。
求个点赞！关注！收藏！
