为什么神经网络可以解偏微分方程,是什么原理?
题主一直比较关心神经网络在其他科学领域的应用,比如数学、物理学还有生物学,比如AlphaFold。本次带来的这篇文章傅里叶神经网络算子解偏微分方程就是一个很有意思的方向,其实我自己去年在给美国一个客户做兼职预测数字货币期权价格的时候就用到过这个算法,因为期权领域的Black-Scholes Model也是一个偏微分方程。在想这周写个什么内容时,突然想到这篇文章,当然我不是物理学专业,其实只需要知道怎么用即可,闲话不多说,下面介绍这篇文章吧。
文章地址:Fourier Neural Operator for Parametric Partial Differential Equations
源码地址:https://github.com/neuraloperator/neuraloperator
作者博客:https://zongyi-li.github.io/blog/2020/fourier-pde/
youtube讲解:https://www.youtube.com/watch?v=IaS72aHrJKE
一作是来自加州理工的Zongyi Li博士,获得过英伟达 2023-2024 研究生奖学金,其导师是Anima Anandkumar,本文的通讯作者,同时也是英伟达的机器学习总监。

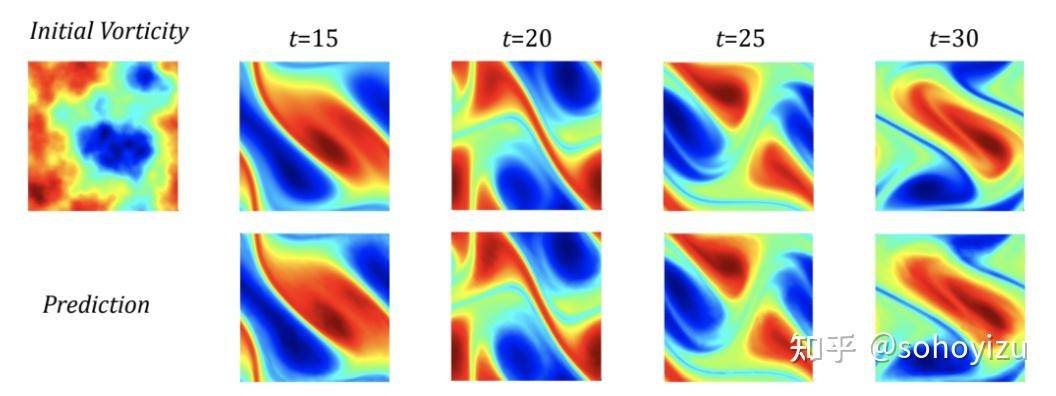
直接上效果,zero-shot超分辨率预测,准确率非常高,说明其FNO无惧分辨率变化-resolution-invariant,它实现了 Burgers 方程的错误率降低 30%,达西流Darcy Flow 降低 60%,Navier Stokes 降低 30%。同时FNO 深度神经网络拥有极快的运行速度。例如,在一个需要进行 30000 次仿真(包括 Navier-Stokes 方程)的求解过程中,对于每个仿真,FNO 花费了不到一秒的时间;而 DeepONet 耗时 2.5 秒;传统的求解器则大概需要花费 18 个小时。
传统的求解器vs 数据驱动的解决方案
有限元法 (FEM) 和有限差分法 (FDM) 等传统求解器通过将空间离散化来求解方程。 因此,需要在分辨率上进行了权衡:粗网格速度快但精度较低; 精细网格准确但速度慢。但复杂的 PDE 系统通常需要非常精细的离散化,因此对于传统求解器来说非常具有挑战性和耗时。 另一方面,数据驱动的方法可以直接从数据中学习方程族的映射mapping。 因此,基于数据驱动学习的方法可以比传统求解器快几个数量级。
算子学习:
神经网络其实就是从有限的输入输出对中学习一种拓展到无限空间的非线性的映射关系,设 是一个有界的开集,
和
是函数的可分 Banach 空间,分别在
和
中取值。 此外,设 G† : A → U 是一个(通常)非线性映射。假设我们有观测值
, 旨在通过构建参数映射,通过选择 θ† ∈ Θ 对于某些有限维参数空间 Θ 来构建 G† 的近似值 使得 G(·, θ†) = Gθ† ≈ G†。
或等效地
,
这是无限维学习的自然框架,因为可以定义成本函数 C : U × U → R 并寻求问题的最小值
对于上面的图可知,算子学习可以看作是图像到图像的问题。 傅里叶层可以看作是卷积层的替代品。
主要解决解决cnn无法实现的resolution-invariant
傅里叶算子
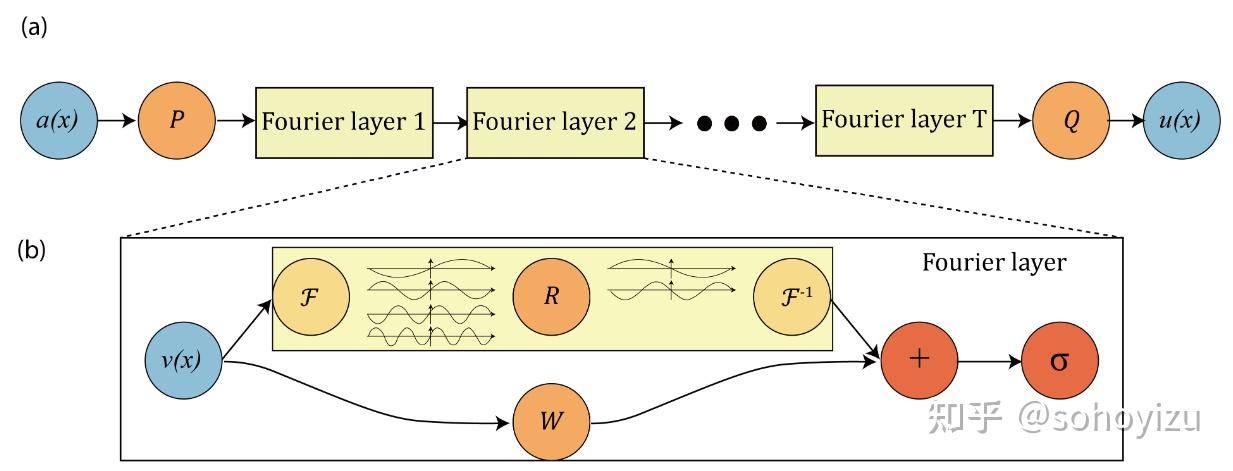
让v 是输入向量,u是输出向量。 一个标准的深度神经网络可以写成以下形式:
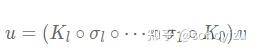
K是线性层或卷积层,σ 是 ReLU 等激活函数。
映射 可以参数化为
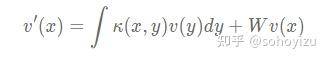
其中 κ 是核函数,W 是偏置项,对于傅立叶神经算子,K 作为卷积并通过傅里叶变换实现。
如图2所示从输入 a 开始。
(1)傅里叶算子结构:
为通过神经网络 P 提升到更高维度的通道空间。 然后应用四层傅里叶积分算子和激活函数。 通过神经网络Q投影回目标维度,输出u。
(2)傅立叶层:
从输入 v 开始。在顶部:应用傅立叶变换 F,对较低的傅立叶模式进行线性变换 R 并滤除较高的模式,然后应用逆傅立叶变换 。 在底部:应用局部线性变换 W 。最后一起过一个激活函数。
FFT变换 和逆变换
可以定义为:
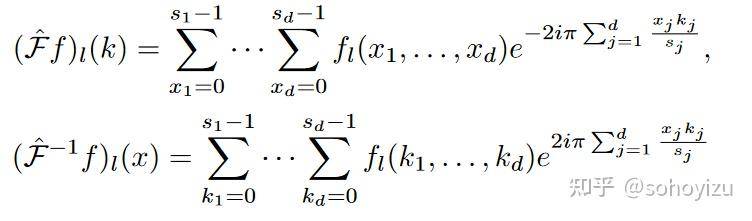
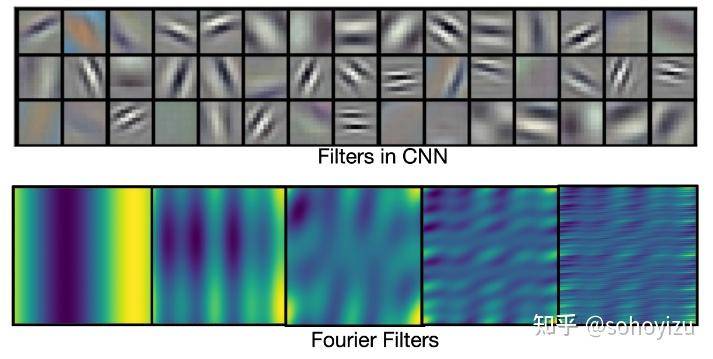
卷积神经网络中的过滤器通常是局部的。 它们很适合捕捉局部图案,例如边缘和形状。 傅立叶滤波器是全局正弦函数。 它们更适合表示连续函数。
高频模式和非周期边界
傅立叶层本身会失去较高频率的模式,并且仅适用于周期性边界条件。 然而,傅里叶神经算子作为一个整体没有这些限制。 傅里叶变换-逆变换结构有助于恢复更高的傅立叶模式。另外偏置项 W 有助于恢复非周期边界。
分辨率不变性
傅里叶层是离散化不变的,因为它们可以从以任意方式离散化的函数中学习和评估。 由于参数是直接在傅里叶空间中学习的,因此在物理空间中求解函数简单地相当于在 的基础上进行投影,而
在
上随处可见,这使FNO能够实现zero-shot超分辨率预估。
简单看一下GitHub中的傅里叶层的代码吧,整体实现不是很难看懂